лог-нормално разпределение
Лог-нормално разпределение - раздел Философия, математическа статистика Случайна променлива Y има логаритмично-нормално разпределение с парам.
Случайна променлива Y има логаритмично нормално разпределение с параметри μ и σ, ако случайна променлива X = lnY има нормално разпределение със същите параметри μ и σ. Познавайки природата на връзката между променливите X и Y, можем лесно да начертаем плътността на вероятността на случайна променлива с логаритмично нормално разпределение (Фигура 4.2).
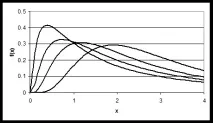
Фигура 4.2 - Криви на плътност на логаритмично нормалното разпределение за различни стойности на параметрите μ и σ
Ако случайна променлива X има функция на плътност на вероятността, дефинирана от формула (4.6), и ако X = lnY, тогава:
, откъдето имаме за y > 0:
(4.14)
От дефиницията следва, че случайна променлива, подчиняваща се на логаритмично нормално разпределение, може да приема само положителни стойности. Както е показано на фигура 4.2, кривите на функцията f(y) имат лявостранна асиметрия, която е по-силна, колкото по-големи са стойностите на параметрите μ и σ. Всяка крива има един максимум и е определена за всички положителни стойности на y.
Изчисляването на математическото очакване и дисперсията на случайна променлива с логаритмично нормално разпределение не е особено трудно:
(4.15)
(4.16)
(4.17)
Чрез замествания и въвеждане на нови променливи в интеграли 4.15 и 4.16 получаваме:
(4.18)
(4.19)
Като цяло, за да се изчисли вероятността случайна променлива Y с логаритмично нормално разпределение и плътност f(y, μ, σ) да приеме стойност в интервала (a, b), трябва да се вземе интегралът:
(4,20)
Въпреки това, наНа практика е по-удобно да се използва фактът, че логаритъма на случайната променлива Y има нормално разпределение. Вероятността a ≤ Y ≤ b е същата като вероятността lna ≤ lnY ≤ lnb.
Нека изчислим вероятността случайна променлива с логаритмично разпределение μ = 1, σ = 0,5 да приеме стойност в интервала (2, 5). Ние имаме:
От таблиците на логаритмите намираме ln2 = 0,6932 и ln5 = 1,6094.
Означавайки lnY = X, можем да напишем:
Освен това случайната променлива X е обект на нормално разпределение със средна стойност μ = 1 и стандартно отклонение σ = 0,5. Сега желаната вероятност може лесно да се изчисли от таблиците на интегралната функция на нормалното разпределение:
Въпроси за самоконтрол
1 Дефиниция на правоъгълно разпределение.
2 Диаграма на плътността на вероятността на случайна променлива с правоъгълно разпределение
3 Фундаментално значение на правоъгълното разпределение.
4 Математическо очакване и дисперсия на случайна величина в правоъгълно разпределение.
5 Ролята на нормалното разпределение в математическата статистика.
6 Какво е нормалното разпределение и как е свързано с биномното разпределение?
7 Графика на плътността на вероятността на случайна променлива с нормално разпределение.
8 Какви статистически параметри могат да се използват за дефиниране на нормално разпределение?
9 Защо нормалното разпределение е непрекъснато?
10 Уравнение на нормална крива.
11 Какво е нормализирано отклонение?
12 Уравнението на камбанообразната крива в нормализирана форма.
13 Какви стойности на μ и σ характеризират нормална популация в нормализирана форма?
14 Какъв процент от пробните данни се вписват в рамките на ±1σ, ±2σ, ±3σ?
15 Какво показва таблицатанормален интеграл на вероятностите?
16 Уравнение на логаритмично нормална крива.
17 График на вероятностната плътност на случайна променлива с лог-нормално разпределение.
18 Какви трансформации трябва да се извършат, за да се получи нормално разпределение от логаритмично нормално разпределение?
19 Какви статистически параметри определят логаритмично нормално разпределение?
ТЕМА 5 Разпределение на параметрите на извадката
5.1 t - Разпределение на Студент
5.2 F-разпределение на Фишер–Снедекор
5.3 χ 2 разпределение
5,1 t - Разпределение на Студент
Нормалният закон на разпределение се проявява, когато броят на характеристиките n>gt; 20-30. Експериментаторът обаче често прави ограничен брой измервания, базирайки заключенията си на малки проби. При малък брой наблюдения резултатите обикновено са близки и рядко се появяват големи отклонения. Това може лесно да се обясни със закона за нормалното разпределение, според който вероятността за поява на малки отклонения е по-голяма от тази на значителни отклонения. Така вероятността за отклонения, превишаващи ±2σ по абсолютна стойност, е 0,05, или един случай на 20 измервания, а отклонения от ± 3σ е 0,01, или един случай на 100.
Ако полевият опит се проведе например в 4-6 повторения, тогава е естествено да се очаква, че няма да има много големи отклонения в показанията на добива на паралелни парцели. Следователно стандартното отклонение s, изчислено за малка извадка, в повечето случаи ще бъде по-малко, отколкото за цялата популация. Следователно в тези случаи човек не може да разчита на нормалните критерии за разпределение в своите заключения.
От началото на 20 век започва да се развива ново направление в математическата статистика, което може да се нарече статистика.малки проби. Най-голямо практическо значение за експерименталната работа има t-разпределението, открито през 1908 г. от английския статистик и химик У. Госет.
Разпределението t на Стюдънт за извадкови средни се дава от:
(5.1)
Числителят на формулата означава отклонението на средната стойност на извадката от средната стойност на цялата съвкупност, а знаменателят:
- е показател, който оценява размера на стандартната грешка на средната извадкова съвкупност.
По този начин стойността на t се измерва чрез отклонението на средната стойност на извадката от средната стойност на популацията, изразена в части от грешката на извадката, взета за единица.
Честотните максимуми на нормалното и t-разпределението съвпадат, но формата на кривата на t-разпределението зависи изцяло от броя на степените на свобода. При много ниски стойности на степените на свобода, тя е под формата на крива с плосък връх, а площта, ограничена от кривата, е по-голяма, отколкото при нормално разпределение, и с увеличаване на броя на наблюденията (n> 30), разпределението t се доближава до нормалното и преминава в него при n = ∞.
Фигура 1.1 показва диференциалното и кумулативното разпределение на t-student за 10 степени на свобода.
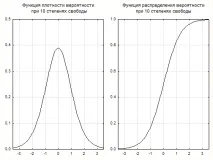
Фигура 5.1 - Диференциално (вляво) и интегрално (вдясно) t-разпределение на Стюдънт
Разпределението на Стюдънт t е важно при работа с малки извадки: то ви позволява да определите доверителния интервал, покриващ средната популация, и да тествате една или друга хипотеза по отношение на генералната съвкупност. В този случай не е необходимо да знаете параметрите на популациятаи, достатъчно е да имате техните оценки μ и σ за определен размер на извадката n.
5.1.1 ПроблемBehrens-Fischer
Тестването на хипотезата за общите средни стойности на две групи с нормално разпределение и неравни дисперсии в математическата статистика се нарича проблем на Беренс–Фишър и в момента има само приблизителни решения. Защо е толкова важно изискването за равенство на дисперсиите в сравняваните групи? Без да навлизаме в подробностите на този проблем, отбелязваме, че колкото повече дисперсиите и размерите на извадката се различават един от друг, толкова повече разпределението на „изчисления t-тест“ се различава от разпределението на „t-теста“. В същото време както самият t-критерий, така и такъв параметър на тези разпределения като броя на степените на свобода имат различна стойност. От своя страна, броят на степените на свобода влияе върху стойността на постигнатото (критично) ниво на значимост (p Fтеор. Теоретичните стойности на F за нивата на значимост 5% и 1% са дадени в таблицата, където само правилните критични точки за F ≥ 1 са таблични, тъй като винаги е обичайно да се намира съотношението на по-голяма дисперсия към по-малка.
Кривите, получени от функцията на разпределение за всички възможни стойности на F, особено за малък брой наблюдения, имат асиметрична форма - дълга "опашка" от големи стойности и голяма концентрация на малки стойности на F (Фигура 5.2).
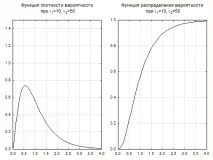
Фигура 5.2 - Диференциал (вляво) и интеграл (вдясно) F-разпределение на Фишер-Снедекор
Обърнете внимание, че t-разпределението на Стюдънт е частен случай на F-разпределението с брой степени на свобода ν1 = 1 и ν2 = ν, т.е. то е равно на броя степени на свобода за разпределението t. В този случай се наблюдава следната връзка между F и t:
(5.3)
5.3 х 2 разпределение
Много действителни разпределения съответстват на модели на теоретични разпределения (нормални, биномни, Поасон) Въпреки това, на практикаима дистрибуции, които са много различни от нормалните. За да се оцени степента на несъответствие или степента на съответствие между броя на действителните и теоретичните разпределения, се въвеждат статистически критерии за съответствие, например критерият χ 2. Този критерий се използва за решаване на проблеми на статистическия анализ, например за проверка на хипотези: относно независимостта на двата принципа, лежащи в основата на групирането на резултатите от наблюдението от един набор; за хомогенността на групите по отношение на определени признаци; относно съответствието между теоретичните и експерименталните криви на изобилие. Критерият χ 2 може да се нарече както критерий за съгласие, така и критерий за независимост, критерий за хомогенност. Законът за разпределение χ 2 (хи-квадрат) е открит от К. Пиърсън. Крива на разпределение, получена от функцията хи-квадрат:
(5.4)
където f са действителните и F са теоретичните честоти на броя на обектите в извадката. Формата му силно зависи от броя на степените на свобода. За малък брой степени на свобода ν, кривата е асиметрична (Фигура 5.3), но с увеличаването на ν асиметрията намалява и при ν = ∞ кривата става нормална гаусиана.
Разпределението χ 2 , също като t-разпределението, е специален случай на F разпределения за ν1 = ν и ν2 = ∞.
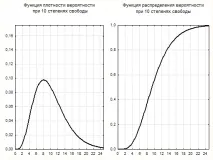
Фигура 5.3 - Диференциално (вляво) и интегрално (вдясно) χ 2 разпределение
Въпроси за самоконтрол
1 Кога е по-добре да се използва t-разпределението на Стюдънт вместо нормалното разпределение?
2 Какви количества трябва да бъдат оценени, за да се използва t-разпределението на Student?
3 Каква е същността на проблема на Беренс-Фишер?
4 Как F-разпределението се изразява числено за две независими проби от общ набор от променливи?
5 От какви характерни количествазависимо от случайни променливи f-разпределение?
6 На какви въпроси може да отговори стойността на критерия χ 2 при статистическата обработка на експериментални данни?