Маркова верига

Определение:

Веригата на Марков(англ.Markov chain) е поредица от случайни събития с краен или изброим брой резултати, характеризираща се с факта, че при фиксирано настояще бъдещето е независимо от миналото.

Процесът е в едно от [math] n [/math] състояния по всяко време.

Освен това, ако е в състояние с число [math] i [/math] , тогава ще премине в състояние [math] j [/math] с вероятността [math] p_ [/math] .

Матрицата [math] P = p_ [/math] се наричапреходна матрица(англ.transition matrix).

На матрицата на прехода се налагат следните условия:

[math] p_ \geqslant 0 [/math]
[math] \forall i\ \ \sum\limits_ p_ = 1 [/math]

Такава матрица се наричастохастична.

Верига на Марков може да бъде представена като графика, в която върховете са състоянията на процеса, а ръбовете са преходи между състояния, а на ръба от [math] i [/math] към [math] j [/math] е написана вероятността за преход от [math] i [/math] към [math] j [/math] , тоест [math] p_ [/math] .

Съдържание

Разпределение на вероятностите[редактиране]

Верига на Марков по всяко време [math] t [/math] може да се характеризира с вектора ред [math] c_t [/math] — вероятностното разпределение върху състоянията на веригата ( [math] c_ [/math] е вероятността веригата в момент [math] t [/math] да бъде в състояние [math] i [/math] ).

Ако [math] c_i [/math] е текущото вероятностно разпределение, тогава можете да намерите разпределението в следващата стъпка, като умножите вектора по преходната матрица:

[math] c_= c_\times P [/math] .

От асоциативността на произведението на матриците следва, че за даза да разберете вероятностното разпределение след стъпките [math] t [/math], трябва да умножите [math] c_i [/math] по матрицата на прехода, повишена на степен [math] t [/math]:

[math] c_= c_\times P^t [/math] .

На веригата на Марков понякога се дава първоначално разпределение [math] c_0 [/math] , въпреки че в много класове вериги на Марков разпределението за дълъг период от време не зависи от нея (такова разпределение се наричаограничаващо(англ.ограничаващо разпределение)).

Достъпност и свързаност[редактиране]

Означете вероятността за преминаване от състояние [math] i [/math] до състояние [math] j [/math] в [math] n [/math] преходи като [math] p_^ [/math] .

Определение:

Състоянието [math] j [/math]е достижимо(на английскиaccesible) от състоянието [math] i [/math], ако съществува [math] n [/math] такова, че [math] p_^ \gt 0 [/math] . Достижимостта на [math] j [/math] от [math] i [/math] се обозначава с [math] i \rightarrow j [/math] .

Определение:

Състоянията [math] i [/math] и [math] j [/math]са докладвани, ако са достъпни едно от друго. Комуникативността на [math] i [/math] и [math] j [/math] се обозначава с [math] i \leftrightarrow j [/math] .

Класификация на вериги и състояния[редактиране]

Неразложима верига[редактиране]

Определение:

Неразложим клас(англ.communicating class) е класът на еквивалентност на набора от състояния по отношение на комуникацията. Ако представим верига на Марков като графика, неразложимият клас ще бъде подобен на силно свързаната компонента.

Определение:

Нередуцируема верига(англ.irreducible chain) е верига на Марков, в която всички състояния образуват един неразложим клас.

Ергодична верига[редактиране]

Определение:

Нека подредим (очевидно подреждането ще бъде частично) неразложими класове по релацията на достижимост. Минималните елементи в такова подреждане се наричат ергодични класове(на английскиergodic classes). Състоянията в ергодичните класове се наричат ергодични(на английскиergodic),повтарящи сеилисъществени(на английскиessential). Всички други неразложими класове се наричат невъзвратими класове. Състоянията, включени в тях, се наричат невъзвръщаемиилиирелевантни(англ.несъществени).

Ако един ергодичен клас се състои от едно състояние, това състояние е поглъщащо. От свойствата на частичното подреждане във всяка верига на Марков има поне един ергодичен клас.

Определение:

Ергодичнаверига на Марков (англ.ergodic Markov chain) е верига на Марков, състояща се изцяло от един ергодичен клас.

Нека [math] N_ [/math] е множеството от [math] n [/math], така че намирайки се в състояние [math] i [/math], човек може да се окаже в състояние [math] j [/math] след [math] n [/math] стъпки. [math] d_i [/math] е най-големият общ делител на числа от множеството [math] N_ [/math] .

Лема:

За [math] i [/math] и [math] j [/math], които принадлежат към един и същ клас на еквивалентност на достижимост, [math] d_i = d_j = d [/math] и числата от набора [math] N_ [/math] са съвпадащи по модул [math] d [/math] .

Доказателство:

[math]\triangleright[/math]

Нека [math] a \in N_, \ b \in N_, \ c \in N_ [/math] . От [math] i [/math] можете да стигнете до [math] j [/math] и обратно, така че [math] a + c \in N_ [/math] . Също така, след като натиснете [math] j [/math], можете да преминете от него към себе си толкова пъти, колкото искате, и едва след това да отидете на [math] i [/math] , за това имате нужда от [math] a + k \cdot d_j + c [/math] стъпки за всеки достатъчно голям [math] k [/math] . Така [math] d_j [/math] трябва да се дели на [math] d_i [/math] . Но по подобен начин може да се докаже, че [math] d_i [/math] се дели на [math] d_j [/math], така че [math] d_i = d_j = d [/math] . Възможно е също да отидете отвъд [math] b [/math] стъпки в [math] j [/math] и след това в [math] i [/math], така че [math] b + c \in N_ [/math] . Така [math] a + c [/math] и [math] b + c [/math] се делят на [math] d [/math], тоест [math] a [/math] и [math] b [/math] са съвпадащи по модул [math] d [/math] .

[math]\triangleleft[/math]

Нека въведем числата [math] t_, 0 \leqslant t_ \lt d [/math] , така че всеки елемент от [math] N_ [/math] да е конгруентен на [math] t_ [/math] по модул [math] d [/math] .

Цикличен клас[редактиране]

Определение:

Цикличен клас(англ.cyclic >[math] i [/math] и [math] j [/math], чието равенство [math] t_ = 0 [/math] .

Определение:

Ако веригата се състои изцяло от един цикличен клас, тя се наричаобикновена, в противен случай —циклична.

Ако веригата е циклична, тя има някакъв период [math] d \gt 1 [/math] и нейните състояния са подразделени на [math] d [/math] цикличникласове. Веригата се движи през цикличните класове в определен ред, връщайки се към класа с първоначалното състояние след [math] d [/math] стъпки.

Топологията на цикличните вериги е разнообразна. Най-тривиалният случай е елементарен цикъл от [math] n [/math] състояния и следователно съдържащ [math] n [/math] циклични класове. По-сложен случай са простите цикли. Простият цикъл се състои от няколко цикъла, които се пресичат във върховете, но не се пресичат в ръбовете. Всички тези цикли не трябва да са взаимно прости. В противен случай gcd на дължините на тези цикли е равна на единица и веригата е правилна. Общият случай на циклична верига е верига, състояща се от цикли, пресичащи се във върхове и ръбове в представянето на веригата като граф.

Примери за циклични вериги[редактиране]

Описание на матрицата за преход на изображението

[math]\begin 0 & 1 и усилвател 0 & \cdots & 0 & 0 & 0 \\ 0 & 0 & 1 и усилвател \cdots & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & 0 & 0 & 1 \\ 1 & 0 & 0 & \cdots & 0 & 0 & 0 \end_N [/math]

Стохастичната матрица на елементарен цикъл винаги има едно 1 във всяка колона и всеки ред. По този начин са необходими точно [math] n [/math] стъпки, преминаващи през всички върхове, за да се стигне от върха [math] j [/math] до него.

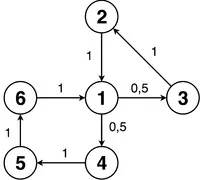[math]\begin 0 & 0 & 0,5 & 0,5 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 и усилвател 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 и усилвател 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 & 0 \end[/math]

Този прост цикъл се състои отдве елементарни, които се пресичат във върха [math] 1 [/math] . Gcd на дължините на всички пътища от върха [math] 1 [/math] до върха [math] 1 [/math] е [math] 1 [/math], така че можете да получите граничното разпределение.

Абсорбираща верига[редактиране]

Определение:

Поглъщащо състояние(англ.absorbing state) е състояние, от което е невъзможно да се премине в друго, т.е. [math] i [/math] е поглъщащо състояние, ако [math] p_ = 1 [/math] .

Определение:

Абсорбтивна(англ.absorbing chain) е верига на Марков, в която има поне едно абсорбиращо състояние и поне едно абсорбиращо състояние е достъпно от всяко състояние.

В примера на фигурата абсорбиращите състояния са [math]3[/math] и [math]4[/math] , докато непоглъщащите състояния са [math]1[/math] и [math]2[/math] .

Пример[редактиране]

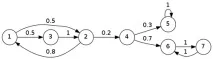
достъпните състояния са: [math] 2 [/math] от [math] 1 [/math] (директно), [math] 3 [/math] от [math] 1 [/math] (директно), [math] 6 [/math] от [math] 3 [/math] (например чрез веригата на състоянията [math] 3 \rightarrow 2 \rightarrow 4 \rightarrow 6 [/math] ) и т.н.
докладват се състоянията [math] 1 [/math] и [math] 2 [/math] (директно), [math] 6 [/math] и [math] 7 [/math] (директно), [math] 1 [/math] и [math] 3 [/math] (достъпни едно от друго) и т.н.
неразложимите класове са наборите от върхове [math] \left \ < 1, 2, 3 \right \>[/math] , [math] \left \ < 4 \right \>[/math] , [math] \left \ < 5 \right \>[/math] , [math] \left \ < 6, 7 \right \>[/math] ;
ергодичните класове са набори от върхове [math] \left \< 5 \right \>[/math] , [math] \left \ < 6, 7 \right \>[/math] ;
абсорбиращото състояние е [math] 5 [/math] състояние.
Ако разгледаме [math] \ [/math] отделно, можем да различим два циклични класа [math] \ [/math] и [math] \ [/math] (на всяка стъпка веригата преминава от едно състояние в друго и след [math] d = 2 [/math] стъпки се връща в същото състояние.

Преброяване на броя на абсорбиращите състояния[редактиране]

Нека [math]\mathtt[/math] е масив от преходи на веригата на Марков, където [math]\mathtt[/math] е вероятността за преход от състояние [math]\mathtt[/math] към [math]\mathtt[/math] . След това, по дефиницията на абсорбиращо състояние, ако [math]\mathtt[/math] е абсорбиращо състояние, тогава [math]\mathtt[/math] . От този критерий е лесно да се определят всички абсорбиращи състояния във веригата.