Метод на геометричното място на точките
Географското място на точките е фигура, която се състои от всички точки на равнината, които имат определено свойство (стр. 61).
Основно GMT от училищния курс по планиметрия:
1. Окръжност: gmt на равнина, която има свойството да е на равно разстояние от дадена точка (П., стр.61).
2. Симетрала на неразвит ъгъл: gmt на еднакво отдалечена от страните на ъгъла равнина (А. стр. 176).
3. Средният перпендикуляр на сегмента: gmt на равнината, равноотдалечена от краищата на сегмента (А., стр. 177, стр. стр. 61).
4. Две прави, успоредни на дадената права и отделени от нея сh: gmt на равнината, отдалечена от дадената права на дадено разстояние.
Същността на метода: задачата се свежда до намиране на точка с две свойства, които следват от изискванията на проблема.
Задача No 688 (А. стр. 181). Дадени са ъгъл и отсечка. Построете точка вътре в дадения ъгъл, на еднакво разстояние от страните му и на равно разстояние от краищата на дадения сегмент.

Разгледайте задача № 39 от учебника на Погорелов (стр. 65): постройте триъгълник по протежение на страната и медианата и височината, начертани към нея.
Анализ. План за застрояване.


2. M е средата на AB.
4. Праваp, успоредна на AB
и на разстояние от него сhc.
6. DABC - желан.
Нека дадем примери за задачи, решени по метода на геометричното място на точките (метод на пресичанията) от учебниците.
Атанасян: 293, 294, 357, 687, 736, 737.
Погорелов: с. 49, № 43; № 44; #45, #45; № 48, параграф 107 № 53.
Подобен метод
Същността на метода е, че въз основа на някои данни се изгражда фигура, подобна на желаната, а след това, използвайки останалите данни, се изгражда желаната фигура.
Задача 3 (А., с. 149, пояснителен текст на учебника).
Изгражданетриъгълник с два ъгъла и ъглополовяща във върха на третия ъгъл.
Условия: РА=a, РВ=b, CL – ъглополовяща РС, CL=lс.

Задача 9 (П., с.102, с.156).
В даден триъгълник впишете квадрат с два върха от едната страна и два други върха от другите две страни.
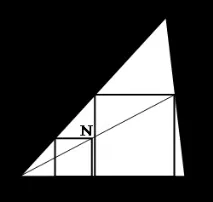
Да разгледаме квадрат, чиито три върха лежат на страните на триъгълника. Такъв квадрат е дефиниран нееднозначно и може да бъде конструиран. KMNP е един от тези квадрати. Желаният квадрат е подобен (хомотетичен) на построения. Върхът му е N1
лежи на лъча AN и страната на триъгълника BC.
Нека дадем примери за задачи, решени по метода на подобието от учебниците.
Атанасян: 587 - 590, 629
Погорелов: т. 102, № 8.