Мини семинар по кристалография 1985 Кантор Б
Мини работилница по кристалография
В заключение на теоретичния минимум по геометрична кристалография предлагаме на читателя няколко упражнения, които могат да се считат за въведение в "практическата" част на кристалографията. Без постоянна практика - това трябва да се подчертае - е немислимо да се изучават дори първоначалните основи на тази наука. Студентите – бъдещи геолози се упражняват върху триизмерни модели на кристали от дърво, картон или пластмаса. Ще трябва да се задоволим със снимки и рисунки, компенсирайки липсата на видимост със собственото си търпение и грижа. Всеки пример трябва да се анализира докрай и да се постигне максимална яснота.
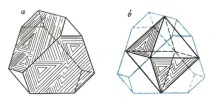
Да започнем с кристал сфалерит. Един от често срещаните навици е показан на фиг. 10, а. Общо има 8 лица на кристала, половината от които са разположени на обратната му страна: 4 еднакви гладки лица и същия брой еднакви лица, покрити с триъгълно засенчване. Наличието на лица с повърхности от два типа предполага, че най-малко две прости форми участват в фасетирането на кристала. Когато набор от лица прилича на проста форма, трябва да се опитате да си представите какъв вид обемна фигура получавате, ако тези лица се продължат, докато се пресекат едно с друго. Тогава останалите прости форми се изключват, така да се каже, и тази форма се получава в чист вид. Извършвайки тази процедура последователно с гладки и пунктирани лица, ние се уверяваме, че и двете прости фигури са равностранни тетраедри, разположени така, че всеки от четирите върха на пунктирания тетраедър е отрязан от едно от четирите лица на гладкия тетраедър. Кристалът трябва да се припише на кубичната система, тъй като равностранните тетраедрине се среща никъде другаде. Всяка от четирите оси L3 минава през центъра на гладката повърхност и центъра на противоположната пунктирана повърхност. Когато двата тетраедъра са развити приблизително еднакво, се получава "фалшив октаедър" (фиг. 10, б). Върху кристалите на сфалерита се срещат и някои други форми на кубичната система.
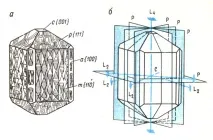
Вилуитният кристал (вид везувиан, Фиг. 11) има една ос на симетрия от 4-ти ред и следователно трябва да се припише на тетрагоналната сингония. Перпендикулярни на L4 са четири оси L2 и равнина на симетрия; още четири равнини на симетрия вървят вертикално, като всяка разделя кристала на две надлъжни огледално равни части. Всички оси и равнини на симетрия се пресичат в една точка, която е центърът на симетрия (фиг. 11, b).
Повърхността на кристала е осеяна с шарки (виж фиг. 11, а), които помагат да се раздели фасетирането на прости форми. Четири широки странични стени образуват тетрагонална призма m, четири тесни странични стени образуват друга тетрагонална призма a, осем наклонени страни на долната и горната глава образуват тетрагонална дипирамида p. Всички тези форми се различават и в скулптурата на лицата. Върховете на дипирамидата са пресечени от две гладки лица на пинакоида c.
В кристал wiluite не е трудно да се очертае аксиален кръст (виж фиг. 11, b). Оста III е съвместима с L4, ос I ще бъде начертана през центровете на две противоположни страни на призмата a, ос II през друга двойка лица на същата призма. Тогава най-близкото лице на призмата a ще бъде успоредно на осите II и III и ще пресича само ос I; следователно призмата a може да се означи със символа . Най-близката страна на призмата m пресича осите I и II под същите ъгли от 45° и е успоредна на оста III; тъй като кристалът е тетрагонален, параметритеелементарна клетка по осите I и II са равни: ao = bо; следователно можем да напишем m . Лицата на дипирамидата p пресичат и трите оси, следователно p. И накрая, пинакоид с две хоризонтални лица ще има символа .

Като минерал от ромбичната кристална система разглеждаме доста рядко срещания минерал рамзаит (фиг. 12). За нашата работилница е удобно за яснотата на кристалната форма. Кристалът е фасетиран от комбинация от пинакоид a, ромбична призма t и ромбична дипирамида s. Вид симетрия - 3L23PC.
Кристалите на арсенопирит, показани на фиг. 13, a и b, са фасетирани от комбинации от ромбични призми m, g, u. Ос I е естествено разположена по ръба на призмата и, ос III - по ръба на призмата m, ос II - перпендикулярна на I и III. Очевидно получаваме ромбична сингония и клас на симетрия 3L23PC, а координатните оси лежат в равнините на симетрия и съвпадат с осите на симетрия. При тази настройка призмата m ще има символа, а призмата g ще има символа. Призмите g и u са ориентирани по един и същи начин (осите им съвпадат), но лицата имат различни наклони спрямо координатните оси; в съответствие с правилата за кристалографско индексиране и се намират.
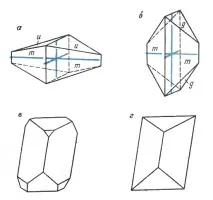
Дълго време арсенопиритът се счита за ромбичен минерал, но с развитието на рентгеновия дифракционен анализ се доказва, че принадлежи към моноклинната система. Това не е единственият случай, когато изследването на кристалната структура е усъвършенствало представянето въз основа на външната форма на кристала. В този случай имаме работа с псевдосиметрия - привидна по-висока симетрия. Има псевдокубични минерали (като ромбичен перовскит), псевдохексагонални (моноклинни слюди и хлорити) и др.
Титанит,или сфен (фиг. 13, c и d) - минералът вече е типично моноклинен. В нашите чертежи титанитните кристали са изобразени в профил, за да се подчертае характерното изкривяване. Моноклинните и като цяло кристалите с ниска симетрия често се отличават с изобилие от прости форми; това може да се види в примера на ортоклазов фелдшпат (фиг. 14). Неговите кристали принадлежат към класа на симетрия L2PC и са фасетирани главно от комбинация от p, M, x, y пинакоиди и ромбична призма T. Има и триклинни фелдшпати. На външен вид те са подобни на моноклинните и разликата е трудно да се хване с просто око. Триклинните фелдшпати са фасетирани само от пинакоиди: призмата T се разделя на два пинакоида d и e.
Време е да обобщим работата си и да си извлечем поука.

Обикновено изследователският арсенал на любителя на минералите е ограничен до 10x или 20x лупа. С негова помощ можете да видите малки кристали, формата и релефа на лицата и други не много малки детайли. Това е много. Видяхме, че формата на различни кристали може да се анализира в непрофесионални условия, без специални инструменти. Нека да разгледаме как го направихме. Ако имахме пред себе си не чертеж, а истински кристал, тогава винаги започвахме с „идеализиране“ му: отклонявайки се от случайни дефекти и изкривявания, допълвайки го с липсващи, но предполагаеми части и т.н. С други думи, ние се опитвахме да заменим кристала с „чертеж“ на идеален кристален полиедър, в който след това открихме елементи на симетрия и разчленихме полиедъра на отделни прости форми. Всички тези техники бяха направени на око, но въпреки това ни позволиха да намерим мястото на кристала в йерархичната стълба на симетрия. Това е изключително важно, когато става въпрос за идентифициране на неизвестен минерал: симетрията е от първостепенно значениедиагностичен знак. В някои случаи дори успяхме да намерим символи за лица и прости форми.
Разбирането на основните закони на формата на кристалните полиедри, практика и умения - това е по същество всичко, което е необходимо за решаване на проблеми, типични в работата на любител на минерали.
Във всички разгледани примери размерите на кристалите са дадени във формат на книжна илюстрация. Такива кристали са ефектни на външен вид и много удобни за изучаване. Но много по-често и професионалният минералог, и любителът трябва да се справят с по-малки кристали. Големи кристали с добро качество са редки (виж таблицата).