Многостепенни системи - Studiopedia
Разгледахме методи, които позволяват да се формират обобщени описания на ситуации в съответствие с решенията, присвоени на ситуациите, включени в обучителната извадка. По време на функционирането на системата работата по формирането на класове ситуации и усъвършенстването на предварително формирани класове се извършва постоянно, тъй като обучителната извадка може да не изчерпи цялото богатство от възможни ситуации, които се развиват върху обекта на управление.
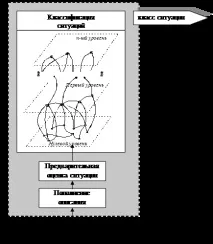

Обобщението може да се случи на много етапи и следователно първоначалните описания на ситуации и техните обобщени описания образуват йерархична структура, във всеки слой от която има описания, получени от първоначалните с помощта на определени процедури за обобщение. Ако първоначалните описания се приемат за нулево ниво, тогава на първо ниво ще има описания, получени директно от описанията на ситуации, лежащи на нулево ниво. Второто ниво ще съдържа описания, които ще възникнат поради прилагането на процедури за обобщение към описанията на първото ниво и т. н. Ето как „пластовата торта“, показана на фиг. 5. Ситуациите на всички нива на обобщение съответстват на някои управленски решения. В идеалния случай на най-високото ниво на класификационната система възникват описания, всяко от които съответства на определено управленско решение. В по-чести случаи, при недостатъчна извадка за обучение, окончателното разделяне на класовете може да не се случи. То никога не се случва в недетерминирания процес на формиране на обобщени ситуации.
Ако самите управленски решения имат някаква структура, тогава при формирането на „слоеста торта“ се изисква да се съпоставят управленските нива в структурата на вземаното управленско решение с нивата на класификатора.
Ако е наличнаконтрол (разтвор)U,, който се състои отnпоследователни контроли, след коетоnнива на класификация се появяват в „слоевата торта“. Йерархията на управление дава възможност да се формират обобщени описания в значително по-малък брой стъпки, отколкото в общия случай.
Такаблокът за обобщение и класификация на ситуациитее многослойна мрежа. При изграждането му се извършва следната последователност от процедури. Първо, първоначалното описание на текущата ситуация се допълва с цялата допълнителна информация поради работата на процедурите за попълване на описанието. След това към получените описания се прилагат процедури за обобщаване. Получените резултати, свързани с първото ниво на "пластовата торта", отново се считат за оригинално описание. Към тях отново се прилагат методи за попълване и се извършва следващата стъпка на обобщаване. Това продължава, докато на следващото ниво към получените фрагменти не могат да се приложат нито процедури за попълване, нито процедури за обобщаване, които не водят до противоречиви управленски решения.
Някои математически методи за обобщаване и процедури за класификация
Алгоритъм на Kora (M.M. Bongard)
ММ. Bongard, анализирайки недостатъците на алгоритъма на персептрон Rosenbalat, предложи някои значителни подобрения на този алгоритъм за проблеми с разпознаването на образи (по-специално геометрични модели, както и "разпознаване" на законите за формиране на аритметични таблици). Като основен недостатък на перцептрона той посочи факта, че връзките на А-елементите с рецепторите не зависят от това каква задача трябва да реши перцептронът - тези връзки се установяват с помощта на партиди, дори преди на перцептрона да бъде показан обучителният материал.
Предложеният от Bongard алгоритъм се състои от 4 блока, коитотой назова: 1)биполярни клетки; 2)ганглиозни клетки; 3)подкортекси 4)кортекс.
Проектирайки структурата на тази схема на Bongard върху нашата задача, можем да установим следното съответствие: 1) биполярни клетки - събиране на първоначални данни за ситуацията (мониторинг); 2) ганглийни клетки - проверка на данни, извършване на прости аналитични операции върху данни; 3) подкортекс - предварителен анализ на ситуацията, трансформация на вектора на характеристиките на всички обекти, 4) кортекс - обобщаване на описанието на ситуациите и приписване на ситуацията към един от известните класове или, ако такова присвояване е невъзможно - формирането на нов клас събития.
Важна характеристика е "многоетажността" на този алгоритъм. В същото време резултатът от обучението на различни нива може да има различна степен на обобщеност (биполярните не учат, ганглийните учат за набор от задачи, подкортексът и кортексът се учат за дадена задача). С този подход, след като се срещне с нова задача, системата започва да преквалифицира горните, най-малко стабилни етажи. И само ако такава преквалификация не даде резултат („светът се промени драматично“), започва преквалификацията на долните етажи.
Очевидно в рамките на задачите, които решаваме, най-голям практически интерес представлява работата на последния от изброените блокове - кората, която всъщност еблок за търсене на правило за разделяне на логическите функции.
На концептуално ниво алгоритъмът на блока "кора" може да бъде представен по следния начин.
1 етап. Този етап не е пряко включен в блока "кора", а е, така да се каже, подготвителен (всъщност това е изходът от блока "подкора"). На този етап се извършва изборът на двоични признаци (преходът от произволни към двоични признаци е теоретично винаги възможен - за това е достатъчно да приемем, че всеки допустимстойността на характеристика действа като независима характеристика или че някои предикати се въвеждат в набора от нейните стойности, които превръщат стойностите си в двоични променливи).
Етап 2. Функциите се генерират произволно от получените двоични аргументи, които също приемат двоични стойности. Всяка такава функция се разглежда като потенциално елементарно правило за разделяне.
Стъпка 3. Изборът на ефективни правила за разделяне, така че за всички отрицателни примери функцията да се превръща в 0, а за положителните примери да се превръща в 1 поне веднъж (но колкото повече, толкова по-добро е правилото за разделяне).
4 етап. Логическото обединение (дизюнкция) на всички ефективни правила за разделяне в едно глобално правило.
5 етап. Проверка (проверка) на глобалното правило върху обучителната проба - проверка на коректността на конструкцията и премахване на излишъка.
6 етап. Проверка на глобалното правило върху изпитната проба. Ако правилото за разделяне не работи правилно върху изпитната извадка, тогава тази проба се счита за допълнителна част от обучителната извадка и процедурата за търсене на правилото за разделяне се повтаря отново (преход към втория етап).
Работата на "основния" алгоритъм се основава на следните принципи.
1) Система, способна да се учи на различен брой примери, трябва задължително да има достатъчно висока първоначална организация. А тази организираност не може да се постигне с предварително обучение. Той трябва да бъде внесен отвън от проектанта на системата.
2) „Кора“ се отнася изключително формално към входящия материал. Тя търси логически функции от всяка от двойките функции, напълно „без да се замисля“ за значението на тези функции. Единственият критерий за търсене е разрезът, произведен от функцията в пространството на характеристиките.
От една страна, това е слабостта на кората. Той проверява всички логически функции от всички двоични характеристики, докато, "разбирайки" тяхното значение, кортексът понякога може да намали изброяването. От друга страна, в такъв необмислен формален подход е източникът на универсалността на кората. Алгоритъмът на кората не зависи от стойността на съдържанието на определен набор от характеристики.
3) Само кратко кодирани параметри влизат в кората. Естествено е същото ограничение да се наложи и на кората. Когато се прилага към кората на разглеждания тип, краткостта означава, че описанието съдържа малък брой връзки. С други думи, описанието на класовете трябва да се състои от малък брой твърдения, свързани с връзка "или". Това налага въвеждането на определени критерии за подбор на обучението:
- връзката, запомнена като знак, трябва да е вярна върху достатъчно голям брой учебни обекти от определен клас (изискването всеки съюз да характеризира много обекти по същество съвпада сизискването за създаване на обобщено описание на класа, а не за запомняне на обекти от учебния материал);
- необходимо е да се провери степента на независимост на различните признаци - във всички случаи разрезът, произведен от "кандидата за характеристика" върху набор от обекти, трябва да се сравни по един или друг начин с разрезите, произведени от вече избраните признаци;
Конюнкция, която характеризира обекти от един клас, не трябва да характеризира обект от друг клас.
4) Където е разумно да се разглеждат обектите като състоящи се в някакъв смисъл от „части“, може да е целесъобразно да се конструират твърдения, базирани както на свойствата на частите, така и на свойствата на обектите като цяло. В тези случаи е целесъобразно да се разглежда многоетажна кора.
По-старата кора се занимава с описания на обекти, а критерият за нея е разделянето на класове. Материалът може да влезе в него директно от оператори, които трансформират целия обект, или от по-млада кора.
Кратките описания на обекта попадат в по-младата кора. Неговата задача е да отдели едни обекти от други и ако това успее, тогава резултатът попада в по-старата кора като нов изходен материал. Имайте предвид, че тъй като критерият за по-младия кортекс не е отделянето на клас от клас, а само разделянето на обектите на две подгрупи, възможно е дори да не се въвежда в него информация за принадлежността на обектите към един или друг клас.
Очевидно, ако е необходимо, е възможно да се конструира кора от трети ранг, четвърти ранг и т.н. В този случай материалът за кората наi-gorang ще бъде или резултат от директна обработка на описанието на части отi-ти ранг чрез оператораразпадане на купчини,или изхода на кората от (i+1)-ти ранг
Не намерихте това, което търсихте? Използвайте търсачката: