наклонени сечения
Коси сечения - Лекция, раздел Философия, Дескриптивна геометрия. Бележки от лекции лекция. Подробности за проекция Нека е необходимо да се изгради естествен разрез на фронтално проектирана равнина.
Нека се изисква да се построи естествен изглед на сечението от фронтално изпъкналата равнина на тялото. Фигура 110а разглежда тяло, ограничено от три цилиндрични повърхности (1, 3 и 6), конична повърхност (7) и сфера (5). В този случай цилиндрите 1 и 6 са ограничени отгоре от равнина 8, а цилиндър 3 е ограничен от двете страни от равнини 2 и 4. Следователно, в допълнение към извитите повърхности, тялото също е ограничено от три равнини (2, 4 и 8), а равнината 8 не се влияе от режещата равнина.
Фигура 110б показва челната проекция на сечението, която съвпада със следата на равнината. Нека построим естествения размер на сечението, като се ограничим само до едната му половина.
Конструкцията се извършва по следния начин:
1) цилиндър 1 е пресечен от режещата равнина по дъгата на елипса, чиято голяма полуос присъства без изкривяване в основния изгледáf́. Тук центърът на елипсата е разположен върху оста на симетрия на основния изглед (точкаf́), а сегментътFGе малката полуос на елипсата, която е равна на радиуса на окръжността на разглеждания цилиндър 1.
За дъгата на тази елипса в сечението построихме четири точки:A- края на голямата ос (върха на елипсата),G- края на малката ос,C- междинна точка иK- точката, в която завършва дъгата на елипсата;
2) линията на пресичане в точкаKпреминава от повърхността на цилиндър 1 до горната основа на цилиндър 3 (към равнина 2).
ОтсечкатаKL от правата линия, по която секущата равнина пресича равнина 2, е показана в пълен размер на плана (KL=kl);
3) от точка L доточка R имаме малка дъга на елипсата, която съответства на пресечната точка със страничната повърхност на цилиндъра 3;
4) тогава пресечната точка минава по праватаRN, която принадлежи на равнина 4 (RN=rn);
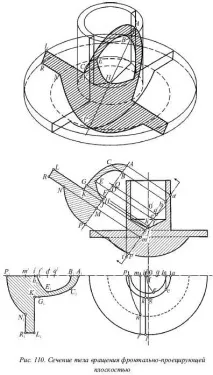
5) по-нататък от равнина 4 пресечната линия преминава към повърхността на топката 5, чийто център е в точкатаO, а центърът на окръжността, по която секущата равнина пресича повърхността на топката, 1 в точкатаQ. В същото време радиусът на тази окръжност еq́ṕ=QP, те трябва да начертаят дъга от центъраQ, докато срещнат линиятаRMв точкатаN(MN=mn);
6) съответно от пресечната точка на секущата равнина с повърхността на цилиндъра 6 трябва да се получи дъга на елипсатаBE. Тук цилиндри 1 и 6 имат обща ос, в резултат на което и двете елипси имат един и същ център в точкатаF;
7) линията на пресичане преминава в точкатаEкъм повърхността на конуса 7, тогава наклонът на секущата равнина спрямо основата на конуса е по-голям от наклона на образуващата. В резултат на това получаваме хипербола с връх в точкатаНи естествен изглед на това сечение е изграден отляво на хоризонталната проекция на фигура 110.
Тази тема принадлежи към категорията:
Дескриптивна геометрия. Бележки от лекции лекция. Относно прогнозите
Информация за лекция за проекции концепцията за проекции четене на чертеж .. централна проекция .. представа за централната проекция може да се получи чрез изучаване на изображението, което човешкото око дава ..
Какво ще правим с получения материал:
Всички теми в този раздел:
Концепцията за проекции Дескриптивната геометрия е наука, която е теоретичната основа на чертането. В тази наука начините за изобразяване наравнини на различни тела и техните елементи
Паралелна проекция Паралелната проекция е вид проекция, която използва успоредни стърчащи лъчи. Когато конструирате паралелни проекции, трябва да зададете
Проекции на точка върху две равнини на проекции Нека разгледаме проекциите на точки върху две равнини, за които вземаме две перпендикулярни равнини (фиг. 4), които ще наричаме хоризонтална фронтална и равнини. Плоска линия на пресичане на данни
Липса на проекционна ос За да обясните как да получите проекции на точка върху модела, перпендикулярна на проекционната равнина (фиг. 4), е необходимо да вземете лист дебела хартия под формата на удължен правоъгълник. Трябва да се огъне между
Проекции на точка върху три проекционни равнини Нека разгледаме профилната равнина на проекциите. Проекциите върху две перпендикулярни равнини обикновено определят позицията на фигурата и позволяват да се установят нейните реални размери и форма. Но има моменти, когато
Координати на точка Позицията на точка в пространството може да се определи с помощта на три числа, наречени нейни координати. Всяка координата съответства на разстоянието на точка от някаква равнина pr
Проекции на линия Необходими са две точки, за да се определи линия. Една точка се определя от две проекции върху хоризонталната и фронталната равнина, т.е. правата линия се определя с помощта на проекциите на нейните две точки върху хоризонталната
Следи от права линия Следа от права линия е точката на нейното пресичане с определена равнина или повърхност (фиг. 20). Хоризонталната следа на линия е точка H
Различни позиции на права Една права се нарича права в общо положение, ако не е нито успоредна, нито перпендикулярна на никоя проекционна равнина. Проекциите на права в общо положение също не са успоредни иперпендикулярен
Взаимно разположение на две прави Има три случая на разположение на прави в пространството: 1) правите се пресичат, т.е. имат обща точка; 2) правите са успоредни, т.е. нямат обща точка, а лежат в една равнина
Перпендикулярни линии Разгледайте теоремата: ако едната страна на прав ъгъл е успоредна на равнината на проекцията (или лежи в нея), тогава правият ъгъл се проектира върху тази равнина без изкривяване. Представяме ви доказателство за
Определяне на позицията на равнината За произволно разположена равнина проекциите на нейните точки запълват и трите проекционни равнини. Следователно няма смисъл да се говори за проекцията на цялата равнина, трябва да се вземат предвид само проекциите
Следи от равнината Следата от равнината P е линията на нейното пресичане с дадена равнина или повърхност (фиг. 36). Линията на пресичане на равнината P с хоризонталната равнина се нарича
Хоризонтали и фронтали на равнината Сред линиите, които лежат в определена равнина, можем да различим два класа линии, които играят важна роля при решаването на различни проблеми. Това са прави линии, които се наричат хоризонтали.
Построяване на следи от равнината Да разгледаме конструкцията на следи от равнината P, която е дадена от двойка пресичащи се прави I и II (фиг. 45). Ако една права е в равнината P, то нейните следи лежат върху едноименните следи
Различни позиции на равнината Равнина в общо положение е равнина, която не е нито успоредна, нито перпендикулярна на която и да е от проекционните равнини. Следите от такава равнина също не са нито успоредни, нито перпендикулярни.
Взаимно разположение на две равнини За две равнини са възможни следните варианти на взаимно разположение: те са успоредни или се пресичат по права линия. От стереометрията е известно, че две равнини са успоредни, ако две
Линия, успоредна на равнина Може да има няколко позиции на една права спрямо определена равнина. 1. Правата лежи в някаква равнина. 2. Правата е успоредна на някаква равнина. 3. Директен трансфер
Права, пресичаща равнина За да се намери пресечната точка на права и равнина, е необходимо да се начертаят пресечни линии на две равнини. Да разгледаме правата I и равнината P (фиг. 54).
Призма и пирамида Помислете за права призма, която стои върху хоризонтална равнина (фиг. 56). Нейните странични зърна
Цилиндър и конус Цилиндърът е фигура, чиято повърхност се получава чрез завъртане на правата линия m около оста i, разположена в една равнина с тази права линия. В случай, че линията m
Топка, тор и пръстен Когато определена ос на въртене I е диаметърът на кръг, тогава се получава сферична повърхност (фиг. 66).
Линии, използвани в чертежа При чертането се използват три основни вида линии (плътни, прекъснати и пунктирани) с различна дебелина (фиг. 76).
Разположение на изгледи (проекции) В чертежа се използват шест изгледа, които са показани на фигура 85. Фигурата показва проекциите на буквата "L".
Отклонение от горните правила за подреждане на изгледи В някои случаи се допускат отклонения от правилата за конструиране на проекции. Сред тези случаи могат да се разграничат следните: частични изгледи и изгледи, разположени без проекционна връзка с други изгледи.
Броят на проекциите, които определят дадено тяло Положението на телата в пространството, формата и размерите обикновено се определят от малък брой подходящо избрани точки. Ако, когато изобразявате проекция на тяло, обърнете внимание
Въртене на точка около ос, перпендикулярна на равнината на проекциите На фигура 91 е дадена оста на въртене I, която е перпендикулярна нахоризонтална равнина и произволно разположена в пространството точка А. При въртене около оста I тази точка описва
Определяне на естествения размер на сегмент чрез ротация Сегмент, успореден на която и да е проекционна равнина, се проектира върху нея без изкривяване. Ако завъртите сегмента, така че да стане успореден на една от проекционните равнини, тогава можете да дефинирате
Построяването на проекции на фигурата на сечението може да се извърши по два начина 1. Можете да намерите точките на среща на ръбовете на полиедъра с режещата равнина и след това да свържете проекциите на намерените точки. В резултат на това ще се получат проекции на желания многоъгълник. В такъв случай,
Пирамида Фигура 98 показва пресечната точка на повърхността на пирамидата с равнината на фронталната проекция P. Фигура 98b показва фронталната проекция a на точката на срещане на реброто KS с равнината
Наклонени сечения Наклонените сечения се разбират като набор от задачи за изграждане на естествени типове сечения на разглежданото тяло от проектирана равнина. За извършване на наклонен разрез е необходимо да се разчлени
Хипербола като разрез на повърхността на конус от фронталната равнина Нека се изисква да се построи разрез от повърхността на конус, стоящ върху хоризонтална равнина от равнина P, която е успоредна на равнината V. Фигура 103 показва фронталната
Разрез на повърхността на цилиндър Има следните случаи на сечение на повърхността на прав кръгов цилиндър с равнина: 1) окръжност, ако секущата равнина P е перпендикулярна на оста на цилиндъра и е успоредна на основите
Разрез на конична повърхност В общия случай кръглата конична повърхност включва две напълно еднакви кухини, които имат общ връх (фиг. 107c). Генераторите на една кухина са продължение на
Повърхностна секциятопка Всеки участък от повърхността на топката с равнина е кръг, който се проектира без изкривяване само ако режещата равнина е успоредна на равнината на проекциите. В общия случай ние
Пирамида За да намерите следи от права линия върху повърхността на някакво геометрично тяло, трябва да нарисувате пряка спомагателна равнина, след което да намерите сечението на повърхността на тялото от тази равнина. Желаното ще бъде
Цилиндрична спирала Създава спирала. Помислете за фигура 113a, където точката M се движи равномерно по определена окръжност, която е сечение на кръгов цилиндър от равнината P. Тук тази равнина
Две тела на въртене Методът за изчертаване на спомагателни равнини се използва при изграждане на линия на пресичане на повърхностите на две тела на въртене. Същността на този метод е следната. Извършете помощна равнина
Раздели Има някои определения и правила, които се прилагат за разделите. Разрезът е плоска фигура, получена в резултат на пресичането на дадено тяло с някои
Раздели Дефиниции и правила, които се прилагат за раздели. Разрезът е такова условно изображение на обект, когато неговата част, разположена между окото на наблюдателя и режещата равнина
Частичен разрез или разкъсване Разрезът се нарича пълен, ако изобразеният обект е изрязан изцяло, останалите разрези се наричат части или разкъсване. На фигура 120, в левия изглед и на плана, са направени пълни разрези. прическа