Намиране на обема на трапецовидна призма - лесно и с примери
Изтрихте изчисления, свързани с обема на трапецовидна призма? Не е нужно да се притеснявате, тъй като бизнес сайтът ще ви предостави начин да намерите неговия обхват с някои примери. Знаете ли, че повечето проблеми с трапецовидни призми включват симетрични форми, т.е. д. височината от всички страни е постоянна. Но при някои призматични дизайни височината може да се различава в различните ръбове, което води до асиметрична трапецовидна призма. Трапецовидната призма е триизмерна геометрична фигура, която се състои от трапец или трапецовидна форма в една част и правоъгълник в друга част. Най-важните компоненти на тази геометрична фигура са нейната дължина, височина, наклон, височина, ширина на основата и ширина на върха. С известните им стойности може да се изчисли обемът и повърхността на трапецовидна призма. Следващият раздел ще ви даде обяснение стъпка по стъпка как да изчислите обема на трапецовидна призма и нейната формула. Най-често изчисленията могат да се направят, ако са известни само долната и горната ширина, височина и дължина. Но когато е известна височината на фаската, вместо действителната височина, тогава трябва да се използва друга формула. Обемът на трапецовидната призма
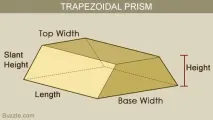
P - Горна ширина
Q - долна ширина В случай, че наклонената височина е дадена вместо действителната височина, тогава формулата за изчисляване на обема е: Обем (V) = L x (p+Q) x √(конфигурация 4s2+ 2PQ - B2 - P2)/4 ---- (Уравнение 2)
където s са височина на изкривяване Други стойностиимат същите имена, споменати в първата формула. Знакът √ показва корен квадратен от цената на скобата.
Прегледайте следните примери, за да разберете как се изчислява обемът на трапецовидна призма. Примери Пример #1 Изчислете обема на трапецовидна призма, която е дълга 7 сантиметра и висока 4 сантиметра. Горната и долната ширина са съответно 3 и 2 сантиметра.
Решение Данните се състоят от:
D = 2 см. Следователно използването на уравненията не е. 1, т.е. д. първата формула, тогава изразът може да бъде записан като: Обем (V) = 7 x 4 x ((3+2)/2) = 28 x 2,5
= 70 Така обемът на призмата е 70 кубични сантиметра (cc). Пример #2A на трапецовидна призма има дължина 5 см и ширина на дъното 11 см. Ширината на горната част е 6 см, а наклонената височина 2 см. Намерете обема на тази геометрична структура.
Решение Данните се състоят от:
M = 6 см. Тъй като действителната височина не е дадена, трябва да използваме уравнение №. 2 за решаване на този проблем. Изразът може да бъде записан като: Обем (V) \u003d 5 x (2 + 6) x √ (4 x (72) + 2 (2 x 6) - 62 - 22) / 4
B \u003d 40 x (√ (196 + 24 - 36 - 4) / 4)
= 268 Така обемът на призмата е 268 cu. сантиметри (cc). Винаги помнете да използвате правилните единици, когато намирате обем, а понякога вместо сантиметри могат да се използват дори инчове и милиметри за изразяване на данни. Също така, в случай на проблеми, при които всички стойности на трапецовидна призма са дадени в различни единици, не забравяйте да ги преобразувате в единица, с която сте запознати, преди да продължите с изчисленията.