Настолни тестове

Знанието е сила. когнитивна информация

Настолни тестове

Нека продължим разглеждането на изпитните тестови задачи.

Тестовете с таблица показват как променливите са свързани една с друга (сумата на променливите е посочена в първата таблица, продуктът е посочен във втората).

В долната част на таблицата е написано какво искате да определите въз основа на данните от задачата.

Универсалният начин за решаване е алгебричен: съставете система от уравнения, решете я, използвайте получените резултати, за да намерите стойността на израза.

Можете да опитате да определите стойността на израза по други начини, без да решавате система от уравнения.

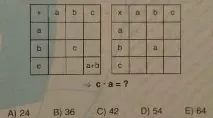
От първата таблица b+b=c, c+c=a+b, т.е. 2b=c, 2c=a+b. От втория - b∙b=a, тоест b²=a.

Имаме система от уравнения:

Заместете c=2b и a=b² във второто уравнение:

2∙2b=b²+b, b²-3b=0, b1=3, b2=0.

Ако b=3, c=2∙3=6, a=a=3²=9, a∙c=6∙9=54.

Ако умножим 1-во и 2-ро уравнение, 2b³=a∙c. Следователно половината от произведението a∙c е кубът на някакво число. От предложените отговори само 54 отговарят на това условие (половината от 54 - 27 - куб 3).

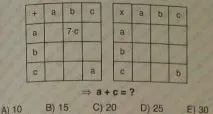
От първата таблица следва, че a+b=7∙c и c+c=a, от втората - c∙c=b. Тоест 2c=a и c²=b. Следователно a+b=2c+c²=7∙c.

Следователно a=0 или a=10.

При c=5, a=10 a+c=15.

(c=0, a=0 не са подходящи).

От първата таблица следва, че b+b=c, т.е. 2b=c, от втората - a∙a=b (т.е. a²=b), a∙b=3∙c.

Умножавайки двете страни на равенството 2b=c по 3, получаваме 6b=3c. Тъй като a∙b=3∙c,

тогава a∙b=6b, откъдето a=6 (за b≠0).

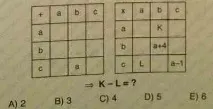
От първата таблица b+c=a, от втората - a∙b=K, b∙b=a+4, a∙c=L, c∙c=a-1. Имаме система от уравнения:

Не е нужно да го решаваме, имаме нуждапросто намери K-L. Извадете член по член от второто уравнение 4-то: ab-ac=K-L, a(b-c)=K-L.

Извадете член по член от 3-то уравнение 5-то:

Тъй като b+c=a, a(b-c)=5.

Следователно K-L=5.

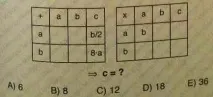
От първата таблица a+c=b/2, b+c=8∙a, от втората - a∙a=b, тоест a²=b.

Извадете второто уравнение член по член от първото уравнение:

a-b=b/2-8a, следователно 9a=3b/2, b=6a. Заместете b=6a в 3-то уравнение: a²=6a. Следователно a=6 (a=0 не е подходящо), b=6a=6∙6=36.

Тъй като a+c=b/2, 6+c=36/2, c=12.

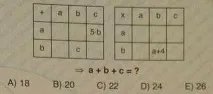
От първата таблица a+c=5b, b+b=c, (т.е. 2b=c), от втората - b∙b=a+4 (b²=a+4). Имаме система от уравнения:

Нека заместим c=2b във второто уравнение: a+2b=5b, откъдето a=3b.

Заместете a=3b във второто уравнение: b²=3b+4, b²-3b-4=0, b1=4, b2=-1.

Ако b=4, c=2∙4=8, a=3∙4=12.

И няколко задачи без таблици.

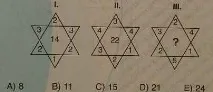
Числото вътре в "звездата" е равно на сумата от произведенията на числата, стоящи в "лъчите" един срещу друг.

III: 3∙1+2∙5+4∙2=21.

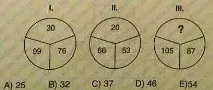
II: 66-53=13, 13+7=20,

III: 105-87=18, 18+7=25.

Следващият път ще разгледаме тестови задачи, в които трябва да намерите периметъра на фигура от чертеж.

---