Нелинейно програмиране, платформа за съдържание

1. Постановка на проблема
2. Метод на множителите на Лагранж
3. Теорема на Кун-Тъкър. Условието за редовност на Слейтър
4. Конвексно и вдлъбнато програмиране
5. Квадратно програмиране
6.1 Постановка на проблема
Проблемът на нелинейното програмиране в общия случай се формулира по следния начин:
при условия
Проблемът с нелинейното програмиране се нарича още проблем на условния екстремум.
За разлика от проблемите на линейното програмиране, няма универсален метод за решаване на проблеми с нелинейно програмиране.
В проблемите на линейното програмиране областта на възможните решенияR(x) винаги е изпъкнала с краен брой крайни точки. Преминавайки само през крайните точки, винаги е възможно да се намери оптималното решение в краен брой стъпки. В проблемите на нелинейното програмиране, нелинейността на ограниченията не винаги гарантира изпъкналостта на областта на възможните решения и крайността на броя на нейните крайни точки. Поради тези характеристики възникват основните трудности при решаването на проблемите на нелинейното програмиране.
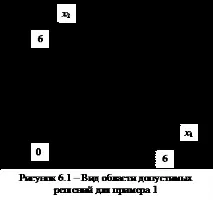
Пример 1. Диапазонът от възможни решенияR(x) се определя от ограниченията:

Областта на възможните решения има формата (Фигура 6.1) и не е изпъкнала.
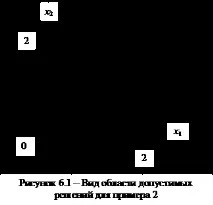
Пример 2. Диапазонът от възможни решенияR(x) се определя от ограниченията:
Областта на възможните решения има формата (Фигура 6.2), е изпъкнала, но има безкраен брой екстремни точки.
6.2 Метод на умножителя на Лагранж
Методът позволява да се намери максимумът (минимумът) на функциятаf(x1,x2, .xn) при ограничения за равенство. Основната идея на метода е преходът от проблема към условния екстремумпроблемът за намиране на безусловен екстремум на специално конструирана функция на Лагранж.
Нека се изисква да се намериminf(x1,x2, .xn)> под ограничения
Да предположим, че функциитеf,g1,g2, .gmса диференцируеми. Въвеждаме набор от променливи l1, l2, . lmот броя на ограниченията, които се наричат множители на Лагранж. Нека съставим функцията на Лагранж със следния вид
За да бъде векторът решение на задачата, е необходимо да има такъв вектор, че двойката вектори да удовлетворява системата от уравнения

По този начин методът на умножителя на Лагранж се състои от следните стъпки:
1. Съставете функцията на Лагранж L(X,L).
2. Съставяме система от уравнения.
3. Намерете неговото решение и изследвайте функциятаf(X) в околността на точкатаX0 върхуmin(max).
6.2.1 Изследване на функция за екстремум
За да бъде стационарната точкаX0 екстремална, е достатъчно матрицата на ХесианHв точкатаX0 да бъде:
Ø е положително определена, тогаваХ0 е точкатаmin;
Ø е отрицателно определен, тогаваX0 е точкатаmax.
За двумерна функцияf(x1,x2), матрицата на Хесиан има формата

За триизмерната функцияf(x1,x2,x3), матрицата на Хесиан има формата

Квадратната формаQ(X) е отрицателно определена, ако стойностите наk-ите ъглови минори на детерминантата ½А½ са различни от нула и имат знак (–1)k(k=1, 2, .n). В този случай матрицатаAсе нарича отрицателно определена.
Квадратната формаQ(X) е положително определена, акостойностите на всички ъглови минори на детерминантата ½A½ са положителни. В този случай матрицатаAсе нарича положително определена.
k-ият ъглов минор на детерминантата на матрицатаA(n´n) е детерминантата на формата

Пример. Нека точката е екстремалната точка на функциятаf(x1,x2,x3) =x1 + 2x3 +x2x3 – . Определете естеството на екстремума?
Нека матрицата на Хесиан има формата

Нека дефинирамеk-ти ъглови минори:

Тъй като матрицата на Хесиан е отрицателно определена, точката е максималната точка.
6.3 Теорема на Кун-Тъкър. Условието за редовност на Слейтър
Условието за оптималност за решаване на задача на нелинейно програмиране е формулирано в теоремата на Кун-Тъкър, която е важна за теорията на нелинейното програмиране.
Теорема. Некаf(X),gi(X) (i=1, 2, .m) имат непрекъснати частични производни върху някакъв отворен набор Вn, съдържащX0. АкоХ0 е минималната точка на функциятаf(X) при ограничения, удовлетворяващи условието за редовност под формата на линейна независимост на векторите , то има такива неотрицателни множители на Лагранж , , . , Какво

Дефинираме функцията на Лагранж по следния начин
Тогава теоремата на Кун-Тъкър може да бъде написана:

Условието за редовност е допълнителни предположения относно естеството на функциитеgi(X) за съществуването на оптимален векторX0. В конкретния случай, когатоf(X) и всичкиgi(X) са изпъкнали функции, условието за редовност има следната форма: съществува векторXтакъв, чеза всичкиi=1, 2, .m. Това условие се наричаусловие за редовност на Слейтър.
6.4 Конвексно и вдлъбнато програмиране
Специален случай на проблем с нелинейно програмиране е проблем с изпъкнало програмиране, който се формулира по следния начин: findminf(X)> при условия
Прилагайки теоремата на Kuhn-Tucker, получаваме следните необходими и достатъчни условия за оптималност: ако функциитеf(X),gi(X) са диференцируеми и изпъкнали по отношение наX, тогава векторътX0 е оптимално решение на задачата за изпъкнало програмиране, ако и само ако съществува такъв вектор, както следва условия:

Проблемът с изпъкналото програмиране се решава по следния начин:
1. Съставете функцията на Лагранж
2. Запишете условието за оптималност под формата на система от уравнения и неравенства.
3. Намерете съвместно решение.
Проблемът на вдлъбнатото програмиране се формулира по следния начин: findmaxf(X)> при условия
Нека покажем, че този проблем е еквивалентен на проблем с изпъкнало програмиране. Нека въведем обозначениетоf*(X) = –f(X) иg*i(X) = –gi(X). Тъй катоmax<f(X)> =minf(X)>, тогава стигаме до проблема:
където всички функцииf*(X) иg*i(X) са изпъкнали вX=x1,x2, .xn>, така че това е проблем с изпъкнало програмиране.
Условията за оптималност се формулират подобно на проблема за изпъкнало програмиране: Нека функциитеf(X),gi(X) са диференцируеми и вдлъбнати вX. За да бъде векторътX0 оптимално решение на проблемаВдлъбнатото програмиране изисква съществуването на вектор, така че да бъдат изпълнени следните условия за векторите за залагане:

По този начин, за да се реши проблемът с вдлъбнатото програмиране, е необходимо да се намери съвместно решение на системата от уравнения и неравенства.
6.5 Квадратно програмиране
Проблемите с квадратично програмиране са специален клас проблеми с нелинейно програмиране, за които целевата функция е квадратична и всички ограничения са линейни.
Тази задача е формулирана по следния начин:
намериmax(min)<f(X)>=BtX+XtCX= при условия
където е симетрична матрица.

МатрицатаCще бъде отрицателно определена в проблема за максимизиране и положително определена в проблема за минимизиране. Това означава, че функциятаf(X) е изпъкнала в променливитеXв проблема за минимизиране и вдлъбната в проблема за максимизиране. Приема се, че ограниченията в този проблем са линейни, което гарантира изпъкналостта на областта на възможните решения.
Прилагайки теоремата на Kuhn-Tucker, получаваме следните необходими и достатъчни условия за оптималност: векторът е оптимално решение на проблем с квадратично програмиране, ако и само ако има такиваm-мерни вектори иn-мерен вектор, че
Първите две условия образуват система от (n+m) линейни уравнения с 2(n+m) неизвестни (векториX0,L0,V0,W0). Третото и четвъртото са условието за допълнителна нетвърдост, което налага допълнителни ограничения върху променливитеX0,L0,V0,W0, а именно:

По силата на тези условия желаноторешението на задачата трябва да бъде едно от допустимите основни решения. За да го намерите, можете да използвате някой от методите на линейно програмиране, например симплексния метод.