Нестабилност на флейта - Студопедия
Една от най-опасните е така наречената флейтова (флейтоподобна в чуждестранната литература) нестабилност. Нарича се още пермутационна или конвективна нестабилност. Тази нестабилност е много опасна, т.к практически не нарушава магнитното поле.
Нека разгледаме тази нестабилност в огледална клетка.
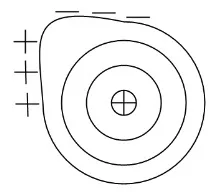
Ориз. 4. Смущение на флейтата
Нека плазмена тръба, опъната по силовите линии, изплува от по-горещ и по-плътен регион към по-малко плътен и по-студен. Разрезът на магнитните повърхности на огледалната клетка, перпендикулярен на оста, е показан на фиг. 4. Това води до извити линии с постоянна плътност. Нека магнитното поле е насочено извън равнината на чертежа. Ако сечението минава през средата на огледалната клетка, магнитното поле в това сечение намалява към периферията. В този случай положително заредените частици се движат в посока на вектора [H,H], т.е. обратно на часовниковата стрелка, а отрицателно заредените частици се движат в обратната посока. В зоната, където тръбата "плува", ще се появят некомпенсирани заряди по нейните краища и ще се появи електрическо поле в полоидална посока. Под действието на това поле както положително, така и отрицателно заредените частици ще претърпят ExB дрейф, което води до по-нататъшно "плаване" на частиците. Но частиците също се движат по силовите линии от запушалката до запушалката, попадайки в онези области близо до запушалките, където магнитното поле се увеличава към периферията. В тези области те ще се отклонят към оста на огледалната клетка. В корковия трон частиците не проникват добре в областта на корка. В резултат на това частиците средно ще се движат навън, т.е. плазмата ще бъде нестабилна.
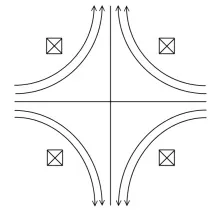
Ориз. 5. Антипробкотрон
В антиогледалната клетка (виж фиг. 5), когато полетата от два пръстенови тока са насочениедин към друг, магнитното поле ще намалява по радиуса навсякъде и плазмата ще бъде стабилна. Но в екваториалния участък в магнитното поле ще има кръгова междина, през която частиците бързо ще напуснат капана по полето. Такава система за ограничаване на плазмата е неподходяща.
Разгледахме качествено нестабилността на флейта. Нека сега се обърнем към неговото количествено описание.
Нека силовата тръба, опъната по силовите линии, „плува“ от позиция 1a–1b до позиция 2a–2b (фиг. 6), като времето за „плаване“ е много по-дълго от времето на полета на частиците между тапите.
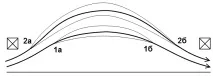
Ориз. 6. Изкачване на тръбата в корковия съд
Тогава при „изплуването” се запазва надлъжният адиабатен инвариант. Изразявайки паралелния компонент на импулса по отношение на магнитния момент и общия импулс, получаваме следния израз за адиабатния инвариант:
. (3.1.1)
Интегрирането тук се извършва между точки на отражение. Когато тръбата се премести от позиция 1 в позиция 2, магнитното поле и точките на отражение се променят. В този случай адиабатният инвариант не се променя:
. (3.1.2)
Нека намерим средната промяна в енергията на частиците за периода:
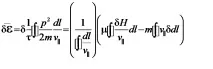
както и изменението на магнитното поле. В инсталации от тип токамак или стеларатор, параметърът, равен на съотношението на плазменото налягане към магнитното, е малък и смущението на магнитното поле може да се счита практически за вакуум, т.е. може да се настрои rotH = 0.6. Ще считаме контура за тесен, т.е. интегралите в сечения 1b–2b и 2a–1a могат да бъдат пренебрегнати. Дължината на участък 1a–1b еdl,магнитното поле в този участък еH.Дължината на участък 2a–2b е , а магнитното поле,съответно е равно на . Така от условието, че циркулацията на магнитното поле изчезва, получаваме
. (3.1.4)
Ако потенциалната енергия се увеличава с отклонение от равновесието, тогава системата е стабилна. Потенциалната енергия на плазма в тръба е сумата от енергиите на всички частици в тази тръба. Вероятността частица да остане върху сегмент от полева линияdlе равна на съотношението на времето на престой в този сегмент към времето на престой между щепселите
Замествайки (3.1.4) в (3.1.3) и отчитайки, че , получаваме
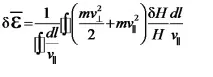
Вероятността частица да остане върху сегмент е равна на съотношението на времето, необходимо за задържане върху него, към периода на въртене между щепселите:
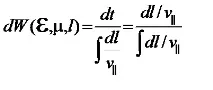
Нека интервалът на дадена полева линия съдържа частици. Тогава общото нарастване на енергията в тръбатаdSима формата
(3.1.7)
Стойността е броят на частиците във фазовото пространствоd 3 pd 3 r.Елементът на обемаdVсе изразява чрез сечението на тръбата и нейния елемент на дължина,dV = dlsS.СтойносттаHdSе магнитният поток през областтаdS.В този случай връзката (3.1.7) се пренаписва, както следва:
. (3.1.8)
В случай на почти изотропна функция на разпределение, може да се напише:
. (3.1.9)
Средноквадратичната скорост на частиците в неподвижна плазма е пропорционална на налягането:
. (3.1.10)
Плазмата ще бъде стабилна, ако енергията й нараства при отклонение от равновесното положение, т.е.
. (3.1.11)
В много реални системи налягането е анизотропно. Най-простият пример за такава система е огледална клетка. Поради бягството през магнитните огледала, разпределението на частиците в паралелни скорости се различава от разпределението в перпендикулярни. В декартовата координатна система тензорът на налягането е диагонален и има формата
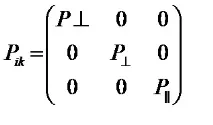
;f– функция
разпределение на скоростта на частиците.
В този случай условието за стабилност (3.1.12) ще изглежда така:
. (3.1.13)
В токамак надлъжното налягане се различава малко от перпендикулярното. Съгласно (1.1.5) трябва да е спазено равенството (H, P) = 0.Следователно условието (2.1.11) става условието
, (3.1.14)
От друга страна, вариацията на интеграла може да бъде представена по следния начин:
,
тъй като в затворени системи стойността не се променя. По този начин условието за стабилност има формата
. (3.1.15)
Тоест интегралът трябва да намалява с разстоянието от оста на системата.
Условието (3.1.15) може да бъде представено малко по-различно:
, (3.1.16)
където е напречното сечение на тръбата, е обемът на тръбата и е магнитният поток през това сечение. Условието за стабилност е намаляването на обема на силовата тръба с нарастването на съдържащия се в нея магнитен поток.
Очевидно е невъзможно да се създаде система с абсолютен минимум магнитен поток. Но е възможно да се създаде система с минимумHсредно. Примери за такива системи са цилиндър с елипсовидно сечение, в което елипсата на сечението се върти около централната ос, и огледална клетка със стабилизиращи пръти (установка на Йофе, фиг. 7).
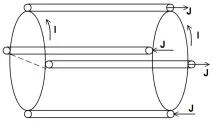
Ориз. 7. Схема на инсталацията на Йофе
Не намерихте това, което търсихте? Използвайте търсачката:
Деактивирайте adBlock! и обновете страницата (F5)много е необходимо