Независими повторни тестове и формулата на Бернули

Формула на Бернули: теория

В този урок ще намерим вероятността за възникване на събитие в независими опити, когато опитите се повтарят. Опитите се наричат ​​независими, ако вероятността за един или друг резултат от всеки опит не зависи от това какви резултати са имали други опити. Независими тестове могат да се провеждат както при едни и същи условия, така и при различни условия. В първия случай вероятността за възникване на събитие във всички опити е една и съща; във втория случай тя варира от опит до опит.

Примери за независими повторни тестове :

• един от възлите на устройството или два или три възела ще се повредят и повредата на всеки възел не зависи от другия възел и вероятността за повреда на един възел е постоянна във всички тестове;
• част, произведена при определени постоянни технологични условия, или три, четири, пет части, ще се окажат нестандартни и една част може да се окаже нестандартна, независимо от всяка друга част, и вероятността частта да се окаже нестандартна е постоянна във всички тестове;
• от няколко изстрела по мишената, един, три или четири изстрела уцелват мишената, независимо от резултата на други изстрели и вероятността за попадение в мишената е постоянна във всички опити;
• когато монетата бъде поставена, машината ще работи правилно един, два или друг брой пъти, независимо от това какви други вмъквания на монети са имали, и вероятността машината да работи правилно е постоянна във всички опити.

Тези събития могат да бъдат описани с една схема. Всяко събитие се случва във всеки опит с еднаква вероятност, която не се променя, ако резултатите от предишни опити станат известни. Такива тестове се наричат ​​независими, а схемата се наричаСхема на Бернули. Предполага се, че такива тестове могат да се повтарят толкова пъти, колкото желаете.

Ако вероятността p за възникване на събитие A във всеки опит е постоянна, тогава вероятността, че в n независими опита събитие A ще се появи m пъти, се намира отформулата на Бернули :

(където q = 1 – p е вероятността събитието да не се случи)

Нека поставим задачата - да намерим вероятността събитие от този тип в n независими опита да се случи m пъти.

Формула на Бернули: примери за решаване на проблеми

Пример 1. Намерете вероятността измежду пет произволно избрани части две да са стандартни, ако вероятността всяка част да е стандартна е 0,9.

Решение. Вероятността за събитие А, състояща се в това, че част, взета на случаен принцип, е стандартна, е p=0,9, а вероятността да е нестандартна е q=1–p=0,1. Събитието, посочено в условието на задачата (означаваме го с B), ще се случи, ако например първите две части се окажат стандартни, а следващите три са нестандартни. Но събитие B също ще възникне, ако първата и третата част са стандартни, а останалите са нестандартни, или ако втората и петата част са стандартни, а останалите са нестандартни. Има и други възможности за настъпване на събитие Б. Всеки от тях се характеризира с факта, че от пет взети части, две, заемащи произволни места от пет, ще се окажат стандартни. Следователно общият брой различни възможности за настъпване на събитие B е равен на броя на възможностите за поставяне на две стандартни части на пет места, т.е. е равно на броя на комбинациите от пет елемента по две и .

Вероятността за всяка възможност, съгласно теоремата за умножение на вероятностите, е равна на произведението от пет фактора, от които два, съответстващи на събитиетостандартни части са равни на 0,9, а останалите три, съответстващи на външния вид на нестандартните части, са равни на 0,1, т.е. тази вероятност е. Тъй като тези десет възможности са несъвместими събития, съгласно теоремата за добавяне, вероятността за събитието B, което обозначаваме

Пример 2. Вероятността машината да изисква вниманието на работник в рамките на един час е 0,6. Ако приемем, че повредите на машините са независими, намерете вероятността в продължение на един час вниманието на работника да бъде изисквано от някоя от четирите машини, обслужвани от него.

Решение. Използвайкиформулата на Бернули за n=4, m=1, p=0.6 и q=1–p=0.4, получаваме

Пример 3. За нормалната работа на автобазата трябва да има най-малко осем вагона на линията, а те са десет. Вероятността за неизлизане на всяка кола от линията е равна на 0,1. Намерете вероятността за нормална работа на депото през следващия ден.

Решение. Автобазата ще работи нормално (събитие F), ако или осем (събитие A), или девет (събитие B), или всичките десет коли влязат в линията (събитие C). Според теоремата за добавяне на вероятности,

.

Намираме всеки членс помощта на формулата на Бернули. Тук n=10, m=8;&nbsp9 10 и p=1-0.1=0.9, тъй като p трябва да означава вероятността кола да влезе в линията; тогава q=0,1. В резултат на това получаваме

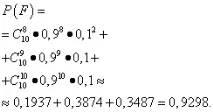
Пример 4. Нека вероятността клиентът да има нужда от мъжки обувки с размер 41 е 0,25. Намерете вероятността от шестима купувачи поне двама да се нуждаят от обувки с размер 41.

Решение. Събитието, посочено в условието на задачата (означаваме го с C) е, че от шест купувачи двама, трима, четири, пет или шест се нуждаят от обувки с размер 41. Чрез прилагане на теоремата за добавяне на вероятности итогава формулата на Бернули, получаваме отговора. Проблемът обаче се решава по-лесно, ако първо потърсим вероятността за събитие, което не се изисква в условието на проблема, а обратното на него. Състои се във факта, че по-малко от двама купувачи се нуждаят от обувки с размер 41, тоест или няма купувач (събитие A), или само един (събитие B). По този начин,

.

Чрезформулата на Бернули при n=6, p=0.25, q=0.75 и m=0; 1 получаваме

(когато изчислявате, имайте предвид това). Тогава вероятността за събитие C се намира като вероятност за събитие, противоположно на намереното:

.

---