Нормална дистрибуция

У дома

цени

Плащане

Примери за решения

Отзиви

Връзки

Теория

Книги

Сътрудничество

Форум

Теория / Теория на вероятностите / 3.5.Нормално разпределение.

§ 3. СЛУЧАЙНИ СТОЙНОСТИ

5. Нормално разпределение.

Казва се, че една случайна променливае нормално разпределенаили се подчинява назакона за разпределение на Гаус, ако нейната плътност на разпределение е

(28)

къдетоaе всяко реално число и>0. Значението на параметритеaще бъде установено по-късно (виж §4, т.2). Въз основа на връзката между плътността на разпределение и функцията на разпределениеF(x)[виж. формула (22)], имаме Графиката на функцията е симетрична по отношение на праватаx=a. Прости изследвания показват, че функцията достига своя максимум приx=aи нейната графика има инфлексни точки при и . При , графиката на функцията асимптотично се доближава до остаOx. Може да се покаже, че когато кривата на плътността на разпределението се увеличава, тя става по-плоска. Обратно, когато намалява, графиката на плътността на разпределението се свива към оста на симетрия. 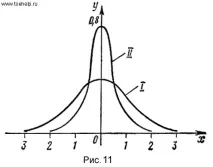Когатоa=0оста на симетрия е остаOy. На фиг. 11 показва две графики на функциятаy=. ГрафикатаIсъответства на стойноститеa=0,=1, а графикатаIIсъответства на стойноститеa=0,=1/2.Нека покажем, че функцията удовлетворява условие (24), т.е. за всякоaи отношението е изпълнено.В действителност ние правим промяна на променлива в този интеграл, настройка . Тогава Поради паритетаинтегранд имаме Следователно, Но, В резултат получаваме

(29)

Намерете вероятността. По формула (23) имаме Нека направим промяна на променлива в този интеграл, отново настройка . След това и

(тридесет)

Както знаем, интегралът не се взема в елементарни функции. Следователно, за да се изчисли определения интеграл (30), се въвежда функцията

(31)

нареченинтеграл на вероятността. За тази функция са съставени таблици с нейните стойности за различни стойности на аргумента (вижте Таблица II на Приложението). Използвайки формула (31), получаваме И така,

(32)

Лесно е да се покаже, че функциятаФ(х)(интеграл на вероятността) има следните свойства. 1°.Ф(0)=02°. ; при , стойността е практически равна на1/2(виж Таблица II). 3°.Ф(-x)=-Ф(х), т.е. вероятностният интеграл е нечетна функция.

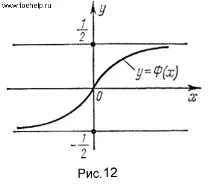
Графиката на функциятаФ(х)е показана на фиг. 12.

Така, ако случайната променлива е нормално разпределена с параметритеaи , тогава вероятността случайната променлива да удовлетворява неравенствата се определя от съотношението (32). Нека>0. Нека намерим вероятността една нормално разпределена случайна променлива да се отклонява от параметъраaпо абсолютна стойност с не повече от , т.е. . Тъй като неравенството е еквивалентно на неравенствата, тогава поставяйки във връзка (32), получаваме Поради факта, че вероятностният интеграл е нечетна функция, имаме

(33)

Пример 1.Нека една случайна променлива се подчинява на нормалния закон за разпределение на вероятностите с параметриa=0,=2. Дефинирайте: (Решение) 1) ; 2) ;

Пример 2.В койтов рамките на ограниченията случайна променлива, подчиняваща се на нормалния закон за разпределение, трябва да се промени, за да (Решение)

От последния пример следва, че ако една случайна променлива се подчинява на нормалния закон за разпределение, тогава може да се твърди с вероятност, равна на0,9973, че случайната променлива е в интервала . Тъй като тази вероятност е близка до единица, можем да предположим, че стойностите на нормално разпределена случайна променлива практически не излизат извън границите на интервала. Този факт се наричаправило на трите сигми.

---