Обратен пиезоелектричен ефект - Радиоелектроника
2. Обратен пиезоелектричен ефект
Наред с пиезоелектричния ефект има и противоположно явление: в пиезоелектричните кристали появата на поляризация е придружена от механични деформации. Следователно, ако върху металните пластини, фиксирани върху кристала, се приложи електрическо напрежение, тогава кристалът се поляризира и деформира под действието на полето.
Лесно се вижда, че необходимостта от съществуването на обратен пиезоелектричен ефект следва от закона за запазване на енергията и наличието на директен ефект. Помислете за пиезоелектрична плоча (фиг. 5) и приемете, че я компресираме с външни сили F. Ако нямаше пиезоелектричен ефект, тогава работата на външните сили би била равна на потенциалната енергия на еластично деформирана плоча. При наличие на пиезоелектричен ефект върху плочата се появяват заряди и възниква електрическо поле, което съдържа допълнителна енергия. Според закона за запазване на енергията следва, че при компресиране на пиезоелектрическата плоча се извършва много работа, което означава, че в нея възникват допълнителни сили F1, които противодействат на компресията. Това е силата на обратния пиезоелектричен ефект. От горните разсъждения следва връзка между признаците на двата ефекта. Ако и в двата случая знаците на зарядите на лицата са еднакви, то знаците на деформациите са различни. Ако, когато плочата е компресирана, зарядите, посочени на фиг. 5, тогава, когато същата поляризация се създаде от външно поле, плочата ще се разтегне.
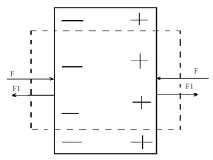
Фиг.5. Връзка между директен и обратен пиезоелектрични ефекти.
Обратният пиезоелектричен ефект има външна прилика с електрострикцията. Тези две явления обаче са различни. Пиезоелектричният ефект зависи от посоката на полето и когато посоката на последното е обърнатасменя знака. Електрострикцията не зависи от посоката на полето. Пиезоелектричният ефект се наблюдава само в някои кристали, които нямат център на симетрия. Електрострикция се среща във всички диелектрици, както твърди, така и течни.
Ако плочата е фиксирана и не може да се деформира, тогава при създаването на електрическо поле в нея ще се появи допълнително механично напрежение, чиято стойност s е пропорционална на силата на електрическото поле вътре в кристала:
където е същият пиезоелектричен модул, както в случая на директен пиезоелектричен ефект. Минусът в тази формула отразява съотношението на признаците на директния и обратния пиезоелектрични ефекти, посочени по-горе.
Общото механично напрежение вътре в кристала е сумата от напрежението, причинено от деформацията, и напрежението, причинено от електрическото поле. Равно е
Тук C е модулът на еластичност при едностранна деформация на опън (модул на Young) при постоянно електрическо поле. Формули (51.2) и (52.2) са основните отношения в теорията на пиезоелектричеството.
Когато пишехме формули, избрахме u и E като независими променливи и считахме D и s за техни функции. Това, разбира се, не е необходимо и бихме могли да разглеждаме като независими променливи друга двойка величини, едната от които е механична, а другата електрическа. Тогава също ще получим две линейни отношения между u, s, E и D, но с различни коефициенти. В зависимост от вида на разглежданите проблеми са удобни различни форми на писане на основните пиезоелектрични отношения.
Тъй като всички пиезоелектрични кристали са анизотропни, константите , C и зависят от ориентацията на повърхностите на плочата спрямо кристалните оси. В допълнение, те зависят от това дали страничните повърхности на плочата са фиксирани или свободни (те зависят от граничните условия придеформация). За да дадем представа за порядъка на големината на тези константи, представяме техните стойности за кварц в случая, когато плочата е изрязана перпендикулярно на оста X и нейните странични повърхности са свободни:
=4,5; C=7.8 10 10 N/m 2; =0,18 C/m2.
Нека сега разгледаме пример за прилагане на основните отношения (4) и (5). Да приемем, че кварцова плоча, изрязана, както е посочено по-горе, е опъната по оста X и плочите, докосващи лицата, са отворени. Тъй като зарядът на плочите преди деформация е равен на нула, а кварцът е диелектрик, тогава след деформация плочите ще бъдат незаредени. Според определението за електрическо изместване това означава, че D=0. Тогава от съотношението (4) следва, че при деформация вътре в плочата ще се появи електрическо поле със сила
Замествайки този израз във формула (5), намираме за
механично напрежение в плочата
Напрежението, както при липсата на пиезоелектричен ефект, е пропорционално на напрежението. Въпреки това, еластичните свойства на плочата сега се характеризират с ефективния модул на еластичност
С' == С (1 + 2 /0С). (8)
което е по-голямо от C. Увеличаването на еластичната твърдост се дължи на появата на допълнително напрежение по време на обратния пиезоелектричен ефект, което предотвратява деформацията. Влиянието на пиезоелектричните свойства на кристала върху неговите механични свойства се характеризира с количеството
Квадратният корен от тази стойност (K) се нарича електромеханична константа на свързване Използвайки горните стойности на , C и , намираме, че за кварц K 2
0,01 За всички други известни пиезоелектрични кристали K 2 също е малък в сравнение с единица и не надвишава 0,1.
Нека сега оценим големината на пиезоелектричното поле. Да приемем, че към лицата на кварцовата плоча, перпендикулярни на оста X,приложено механично напрежение 1 105 5 N/m 2 . Тогава съгласно (7) деформацията ще бъде равна на u=1,3 10 - 6 . Замествайки тази стойност във формула (6), получаваме E==5900 V/m=59 V/cm. При дебелина на плочата, да речем, d==0,5 см, напрежението между плочите ще бъде равно на U=Ed
30 V. Виждаме, че пиезоелектричните полета и напреженията могат да бъдат доста значителни. Чрез използване на по-силни пиезоелектрици вместо кварц и използване на правилно избрани видове деформация могат да се получат пиезоелектрични напрежения, измерващи много хиляди волта.
Пиезоелектричният ефект (директен и обратен) се използва широко за конструирането на различни електромеханични преобразуватели. За това понякога се използват композитни пиезоелементи, предназначени да извършват различни видове деформации.
Фигура 6 показва двоен пиезоелектричен елемент (съставен от две плочи), работещ при компресия. Плочите се изрязват от кристала по такъв начин, че да се компресират или разтягат едновременно. Ако, напротив, такъв пиезоелектричен елемент се компресира или разтяга от външни сили, тогава между неговите плочи се появява напрежение. Свързването на плочите в този пиезоелектричен елемент съответства на паралелното свързване на кондензатори.
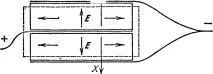
Ориз. 6. Двоен пиезо елемент, работещ при компресия.
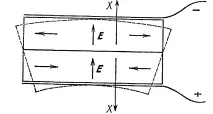
Фиг.7. Двоен пиезо елемент, топящ се в огъване. РЕФЕРЕНЦИИ.
“Електричество” С.Г. Калашников, Москва, 1977 г
“Електротехнически материали” Ю.В. Корицки, Москва, 1968 г
„Радиопредавателни устройства“ G.A. Цайтленка, Москва, 1969 г