Определяне на размера на порите на мембраната по метода на точката на кипене

Точката на кипене е минималното налягане на газа, необходимо за екструдиране на течност от порите на максималния диаметър на мембраната. Методът на "точката на кипене" е разработен от Behold в началото на века.

Основава се на ефекта на капилярността (виж фиг.1), според който височината на водния стълб в капиляра е обратно пропорционална на диаметъра на последния. Водата се задържа в капиляра от силите на повърхностно напрежение и ако диаметърът на капиляра намалее, височината на водния стълб ще се увеличи. Но водата, която се е издигнала до определена височина в капиляра, може да бъде върната обратно чрез налягане, чиято стойност е еквивалентна на височината на водния стълб в капиляра. Следователно чрез измерване на налягането, при което водата се измества от капиляра, може да се изчисли неговият диаметър. Приложено върху мембрана, то би изглеждало така: Горната част на мембраната е в контакт с течност, която запълва всички пори на мембраната, ако условието за намокряне е изпълнено. Долната част на мембраната е в контакт с въздух (газ) и с постепенно увеличаване на налягането на въздуха въздушно мехурче ще проникне през порите (при условие че радиусът на мехурчето е равен на радиуса на порите) (виж фиг. 2). Тези. мембранен филтър, наситен с течност, не пропуска въздух (газ) при тези налягания, които осигуряват филтрирането му през сух филтър (дифузионен газов поток). Въпреки това, когато налягането се увеличи, се достига състояние, при което силата на повърхностното напрежение в големите пори се преодолява и течността се изтласква от тези пори (обемен газов поток) (виж фиг. 3). Същността на метода е да се измери налягането, необходимо за преминаване на въздуха през мембраната (началото на обемния поток от газ), пълна с течност, която се омокря по отношение на нея. Трябва да се отбележи, че изтичането на газ през намокрената мембранаще се наблюдава основно през най-големите пори, чийто радиус може да се изчисли с помощта на уравнението на Лаплас:D = 4∙γ ∙(cosθ) /P, (1)

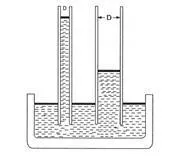
къдетоD е диаметърът на пората с капилярна форма (µm),γ е повърхностното напрежение на границата течност-въздух (за вода 72 dynes/cm)θ е контактният ъгъл на намокряне (моментът на пробив на газа означава, че контактният ъгълθ е равен на нула (cos θ = 1 ))Р – точка на кипене. Т.е. В случай на вода това уравнение приема формата:

D = 221.3 / Р, къдетоР – измерено в cmHg. От формула (1) следва, че методът на точката на кипене не зависи от естеството на приложената течност. Известно е обаче, че при определяне на порите в една и съща мембрана с помощта на различни омокрящи течности: вода, метанол, етанол, n-пропанол, изопропанол, дава различни резултати. Това явление е слабо разбрано, вероятно поради ефектите на овлажняване. Поради това бяха избрани няколко по-стандартни омокрящи течности. В случай на измерване на много малки пори, ако се използва вода като омокряща среда, налягането, при което се достига точката на кипене, може да бъде толкова високо, че да настъпи деформация на мембраната, което обезсилва резултатите от измерването. Следователно, за да се получат надеждни резултати от измерването, трябва да се използват течности с повърхностно напрежение, по-ниско от това на водата. Най-разпространеното в случая е минералното масло със стойност на повърхностното напрежение 34,7 dynes/cm. В този случай уравнението на Лаплас приема формата:

D = 106 / Р къдетоР – измерено в cmHg. За мембрани с дори по-малки размери на порите се използва друга омокряща течност, изобутанол. Силата на повърхносттанапрежението на изобутанола е 1,7 dynes/cm, което прави възможно измерването на пори 40 пъти по-малки от намокряне с вода. В този случай обаче трябва да се гарантира, че материалът на мембраната е химически съвместим с изобутанол. Строго погледнато, всички горни аргументи и формули за определяне на размера на порите по метода на мехурчетата са валидни само ако порите имат цилиндрична форма. В практиката по-често се срещат мембрани с извита пореста структура. Освен това в повечето случаи напречното сечение на порите прилича повече на елипса, отколкото на кръг. Възниква въпросът: Какво тогава съответства на обозначенията за размер на порите, поставени от производителите на мембрани, тъй като при масовото производство на мембрани размерът на порите им не се измерва, а се изчислява с помощта на математически модели, базирани на теорията за капилярността. Тези. възниква дилема. Размерите на филтриращите частици измерваме директно - под микроскоп, а точката на кипене се определя индиректно от хидродинамиката. И все пак почти всички производители посочват точния размер на порите на мембраните.

Тъй като формата на порите оказва значително влияние върху измерената стойност на налягането в точката на кипене, производителите на мембрани прибягват до всякакви „изобретения“. А именно, в числителя на нашия първоначален израз (1) се въвежда известна корекция, която отчита формата на порите. Нека наречем тази корекция k. Обикновено производителите не посочват как се получава този коефициент, но е известно, че той обикновено се получава емпирично за всеки тип мембрана. Възможно ли е теоретично да се получи израз, свързващ точката на кипене и размера на некръгла пора? Оказва се, че да. Първоначалните данни ще бъдат фактът, че в нашия случай измерването на точката на кипене включва две противоположно насоченисили: първата (положителна) е силата на повърхностното напрежение; вторият (отрицателен) е хидростатичен. Първият, както е известно, е свързан с размерите на пората (периметъра) чрез коефициента на повърхностно напрежение и ъгъла на намокряне. Вторият е чрез приложената сила (налягане на газ). В точката на балона тези противоположни сили са равни. Тези. може да се напише, че:

(площ на напречното сечение на порите)γ ∙cosθ = (площ на напречното сечение на порите)∙ Р (2)

Както е известно от геометрията, елипсата има две оси (вижте фигурата) - малка (b) и голяма (a). В този случай размерът на частиците, които могат да преминат през мембраната, зависи от първия. Площта на елипсата е равна на произведението на дължините на голямата и малката полуоси на елипсата и числото pi: (S = π a b). Ако обозначим (по аналогия с кръгла пора, двойната дължина на полуос b до D и двойната дължина на полуос a до D1) и съотношението на D1 към D през E, тогава формулата за изчисляване на площта на елипсата може да бъде записана, както следва:

S = π(D1/2) (D/2) = π(D E/2) (D /2) = (πD2 E)/4 В случай на кръг, E = 1 и от горната формула получаваме формула за изчисляване на площта на кръг. Подобно разсъждение, извършено във връзка с формулата за приблизително изчисляване на периметъра на елипса, ще ни даде следния израз:

L = πD2 [(1+E2)/2 ]1/2

Замествайки получените формули в нашия израз (2) и трансформирайки го по такъв начин, че да можем да сравним резултата с формула (1), виждаме, че уравнението за определяне на диаметъра на порите с елиптично напречно сечение на порите има формата:

И отново, в случай на кръг, E = 1 и получаваме уравнение (1) от горната формула. От този израз следва, че размерът на порите,изчислено от предположението, че има кръгло напречно сечение, винаги ще бъде с 25 до 30% по-голямо от елиптичната пора. Следователно, ако при решаването на проблема с микрофилтрацията се нуждаем от гарантирана степен на стерилизация, а не от висока точност на класифициране на мембраните по размер, тогава очевидно можем да пренебрегнем геометрията на порите и да приемем, че те имат кръгло напречно сечение. И тъй като точната геометрия на порите може да бъде определена само след допълнително трудоемко изследване, като се използва прост метод на точката на кипене за определяне на размера на порите на мембраната, ние имаме допълнителен фактор за безопасност.

---