Организация на изследователската работа на учениците в уроците по математика, В помощ на млад учител

Организация на изследователската работа на учениците в часовете по математика

Изследователската работа е доста сложна дейност както за учениците, така и за тези, които ги ръководят. Според мен изследователското учене е учене, което надхвърля училищния курс, отвъд учебника. Учителите се занимават с такава работа с учениците главно в извънкласни часове: по избори, избираеми курсове, в кръгове. В рамките на урока задачата за развиване на умения за самостоятелно изследване е много трудна за решаване. Стимулирането на изследователската дейност на учениците изисква правилен избор и прилагане на методи на учебна дейност.

Основата на моя опит в организирането на изследователската работа на учениците в часовете по математика беше модел, създаден от група изследователи под ръководството на известния американски дидакт X. Taba. В нейното разбиране образованието има съдържателни и развиващи компоненти. Х. Таба идентифицира три последователни типа образователни (образователни и познавателни) задачи:

Въз основа на това могат да се разграничат три основни етапа на организиране на изследователска работа със студенти:

Формиране на понятия.
Откриване на собственост. Изграждане на изводи и следствия.
Обяснение на нови факти въз основа на свойства.

Този модел предлага балансиран подход към образователния процес, като се стреми към баланс между елементите на съдържанието на обучението, между целенасоченото учене и развитие на ученика, между дейността на учителя и децата.

Училищният курс по математика предоставя големи възможности за организиране на изследователската дейност на учениците в класната стая.

Използвайки примера на уроците по геометрия за 8 клас по темата „Успоредник“, искам да покажа как можетеорганизират изследователска работа на всеки етап.

Ι етап. Формиране на концепция

За да включа учениците в изследователска работа, предлагам да изброя обекти (фигури, техните свойства) и да ги комбинирам в групи. За това се задават въпроси. И така, въпросът „Какво видяхте? Забелязал ли си? насърчава децата да изброят тези обекти, въпросът "Какви обекти (фигури и т.н.) са свързани помежду си?" Насърчава децата да комбинират данни в групи.

Имайте предвид, че тези въпроси са отворени, т.е. те не предполагат нито един „правилен“ отговор. Децата не се стремят да „отгатнат какво има в ума на учителя“, те провеждат активно интелектуално търсене.

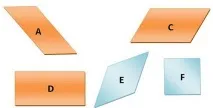
Задача 1. Предлагам момчетата в групи от по 4 души да изпълнят задачата. Всеки ученик има два равни правоъгълни триъгълника.

Направете четириъгълник от два правоъгълни триъгълника. Намерете различни начини за решаване на този проблем.

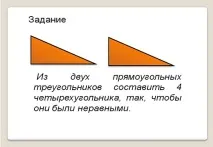
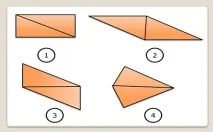
- Как мислите, коя фигура е излишна тук? Защо смятате, че е излишно?

Тук мненията на студентите се различават. Някой избира 1 фигура, други 4-та фигура.

Разберете какво представлява всяка от фигурите. Каква е разликата между 1-ва фигура и 4-та?

Оказва се, че първите три фигури са познати на момчетата, но те не знаят последната цифра. При позоваване на учебника тази фигура не е намерена.

Така се въвежда нова фигура - делтоидът, който не се изучава в училищния курс. Учениците успоредно с останалите четириъгълници изследват тази фигура.

Задача 2.

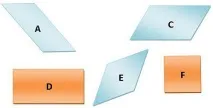
- Фигурата показва четириъгълници. Елиминирайте излишъка. Защо? Този четириъгълник се нарича трапец. Откъде идва това име?

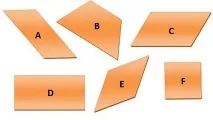
- Какво общо иматеоставащи фигури? Как бихте ги кръстили?

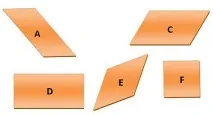
Групирайте успоредниците в 2 групи. На какво основание го направи?

ΙΙ етап. Откриване на собственост. Изграждане на изводи и следствия

След определяне на класа на обектите, които се изследват, задачата е да се намерят, „открият“ други общи свойства на обектите, които се разглеждат. При разглеждане на свойствата на изследваните обекти учениците се поставят в позицията на „откриватели на свойства“, насърчавани да правят предположения за наличието на определени свойства.

Обикновено етапът започва с уводен въпрос на учителя, насочен към припомняне на вече известни данни. Например „Какво научихте за успоредник, трапец или делтоид?“. Цялата информация се събира; всичко, което може да бъде представено във визуална форма (фигури, таблици), се излага на публичен показ. Учителят насърчава децата да правят изявления, но в никакъв случай не ги бърза - всички изявления на децата се приемат във формата, в която са изразени, и учителят не бърза веднага да ги преведе във формата, която му се струва по-приемлива. Следват интерпретативни въпроси: „Какво ще се случи, ако…“, „Какво се случи, когато…“, „Може ли да бъде…“.

- Какво ще стане, ако начертаем ъглополовяща в успоредник, две ъглополовящи от два едностранни ъгъла, две ъглополовящи от противоположни ъгли ...

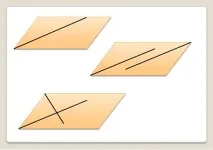
Ето една от хипотезите, формулирани от ученик в урок по геометрия в 8 клас, докато изучаваше темата „Ако начертаете ъглополовящите на ъглите на успоредник, тогава те, пресичащи се по двойки, образуват успоредник.“ След като изложи тази хипотеза, студентът завърши рисунката.

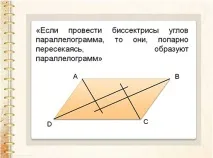
„Оказва се не просто успоредник, а правоъгълник!“ След това момчетата започват да търсят доказателства. При това те използват предишнотопроучвания (по-специално, ъглополовящите, изтеглени от едностранни ъгли, са взаимно перпендикулярни, а ъглополовящите, изтеглени от противоположни ъгли, са успоредни).

Какво ще стане, ако свържем последователно средите на страните в успоредник?

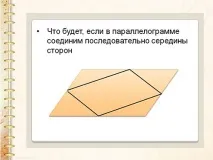
Получаваме още една фигура за изследване, която не се изучава в училищния курс по геометрия: успоредникът на Вариньон.

Всички задачи, измислени от учениците по време на учебния процес, се представят за обсъждане в Деня на геометрията, който се провежда ежегодно в края на учебната година под мотото „Който не знае геометрия, да не отваря тук вратата“.

ΙΙΙ етап. Обяснение на нови факти въз основа на свойства

Този етап се основава на насърчаване на децата да обясняват нови явления.

Уводният мотивиращ въпрос на учителя може да бъде от абстрактно абстрактно теоретичен характер: "Какво ще се промени, ако ...", "Какво ще стане, ако ...". Например, когато работите върху определянето на характеристиките на фигура, можете да зададете следния въпрос: „Какво се случва, ако условието и твърдението са обърнати?“. И така, учениците формулират твърдение, което е обратното на свойството. В последната фаза на стратегията учениците проверяват своите предположения, хипотези, заключения или посочват условията, при които може да се направи тест.

С такава работа учениците могат да формулират признаци, които не са формулирани и доказани в училищните учебници.

Например, според свойствата на успоредник, неговите нови знаци се „появяват“: „Ако противоположните ъгли на четириъгълник са равни, тогава този четириъгълник е успоредник“.

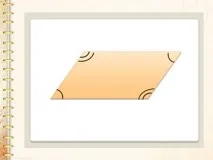
Подобна работа може да се организира и по други теми от геометрията за 8 клас.

Теми на научните работи по геометрия 8 клас

По време на изучаването на тези теми иманаучни статии, които надхвърлят училищния курс по математика. Ето само няколко от тях:

Делтоид
триъгълник на педала
Успоредник на Вариньон
невероятен квадрат
Вписани и описани окръжности
Вписани и описани четириъгълници

В заключение ще се опитам да отговоря на два важни според мен въпроса.

Какво дава на детето участието в изследователска дейност?

ранно разкриване на интереси и склонности към научноизследователска дейност;
задълбочена подготовка за самостоятелна изследователска работа;
ранна професионална ориентация;
допълнителен опит в публичното говорене.

Какво дава организацията на изследователската дейност на учителя?

осъзнаването на учителя за необходимостта от професионално израстване (преди да преподава на детето изследователска дейност, учителят трябва да се учи сам);
получаване на условия за повишаване на квалификацията на учител (организиране на лекции за учители, възможност за участие в работата на журито, присъствие на защита, слушане на доклади);
И накрая, това е просто забавно!