Основни принципи на доказателство за блок-схеми
По този начин, за прости програми с един цикъл, основните трикове за доказване на коректността на блок-схемите са:
1) доказателство, че при достигане на входната точка на цикъла, някое твърдение (инварианта на цикъла) винаги ще бъде вярно. За да докажем това, ние показахме, първо, че това твърдение е вярно, когато за първи път достигне входа на цикъла, и, второ, ако достигнем тази точка и твърдението е вярно, тогава след изпълнение на цикъла и връщане към входната точка, твърдението ще остане вярно;
2) доказателство, че ако твърдението, което е инвариант на цикъла, и твърдението за крайността на цикъла са изпълнени едновременно, твърдението за коректността на програмата автоматично следва от инварианта на цикъла.
Нека илюстрираме тези идеи с доказателство за коректност за блок-схема на много проста програма.
ПРИМЕР 2. Да предположим, че трябва да изчислите произведението на произволни две цели числаM,NиM³0 и операцията за умножение не може да се използва. За да направите това, можете да използвате операцията за събиране и да изчислите сумата отMчленове (всеки е равен наN). В резултат на това получавамеM∙N. Помислете за блокова диаграма, която реализира такова изчисление (фиг. 2.1). Необходимо е да се докаже, че дадената програма изчислява правилно произведението на произволни две цели числаMиNпри условиеM³0, т.е. ако програмата се изпълнява с цели числаMиN, къдетоM³0, тогава тя в крайна сметка ще завърши (достигайки точка 5) със стойносттаJ=M∙N.
За да представим по-ясно етапите на доказателството за коректност, ще "припишем" ключовите твърдения, които трябва да бъдат доказани директно към точките от блоковата диаграма, за които се отнасят (фиг. 2.2).
Забележка: доказвайки валидността на определено твърдение в момента на преминаване през която и да е от точките на вътрешния цикъл (инварианта на цикъла), ще използваме принципа на простата индукция и ще приемем, че трябва само да покажем, че: 1) твърдението е вярно, когато за първи път удари тази точка, и 2) ако ударим тази точка и в този момент твърдението е вярно, след което цикълът се изпълнява и ние отново се връщаме в началната точка, тогава твърдението ще отново да е истина. (т.е. по-просто е: изпълнението на цикъла не нарушава истинността на твърдението - инвариантът на цикъла.) Ако сме доказали и двете твърдения, тогава, възстановявайки необходимите подробности, можем да докажем чрез индукция върху броя преминавания през точката, че първоначалното твърдение е вярно за всяко попадение в дадена точка.
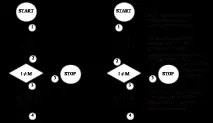 |
Фиг. 2.1 Фиг. 2.2
Нека сега докажем, че показаното на фиг. 2.2 блоковата диаграма е правилна, т.е. ако започне да се изпълнява сMиN, имащи някои цели числа, иM³0, тогава изпълнението в крайна сметка ще завърши сJ=M ∙ N.
Първо доказваме, че при удар в точка 2,J=I ∙ N.
1. При първото попадение в точка 2, при преминаване от точка 1, имамеI= 0 иJ= 0. Така твърдениетоJ=I ∙ N= 0∙ N= 0 е вярно.
2. Да приемем, че сме достигнали точка 2 и твърдениетоJ=I ∙ Nе вярно. НекаIиJв този момент приемат стойноститеInиJn, т.е.Jn=In∙ N. АкоI¹Mе невярно, тогава това вече предоставя крайния резултат. Нека сега приемем, че сме преминали през цикъла (от точка 2 през точки 3, 4 отново до точка 2), което е възможно само ако условиетоI№M. Когато се върнете към точка 2,IиJприемат нови стойностиIn+1 иJn+1, които могат да бъдат представени по следния начин:
Следователно, при повторно постигане на точка 2 твърдениетоJ=I∙ Nотново е вярно, което трябваше да бъде доказано, т.е. при попадение в точка 2 твърдениетоJ=I ∙ Nе вярно.
Сега нека докажем, че в крайна сметка стигаме до точка 2 със стойностI=M. При първото попадение в точка 2 имамеI=0. При следващи удари, ако има такива,Iсе увеличава всеки път с 1. Тъй като стойността наMне се променя никъде в програмата и ние предположихме, чеM³0, очевидно е, че в даден моментIще стане равно наM.
Ако стигнем до точка 2 сI=M, тогаваJ=I ∙ N=M ∙ Nсъщо ще бъде вярно. ОтношениетоI¹Mе невярно в този момент и следваме стрелката, отбелязана с F (FALSE – невярно) до точка 5 сJ=M ∙ N. С това приключва доказването на коректността на програмата.
За повече примери за доказване на правилността на блок-схеми за прости програми (с един цикъл), вижте [1].
Упражнение
1. Докажете, че програмата (фиг. 2.3) изчислява произведението наMиNпри условие, чеMиNимат цели числа иM³ 0. Какво се случва, акоMN . Приема се, чеMиNса цели числа и u1 £Mи 1 £N. Ще работи ли тази програма правилно, акоNе зададено на 0? Променете блок-схемата, така че програмата да работи правилно дори когатоN= 0.
4. Докажете, че програмата (фиг. 2.5) изчислява и отпечатва стойносттаM! = 1 × 2 × 3 ×. × (M– 1) ×Mпри условие, че положително цяло число е въведено катоM.
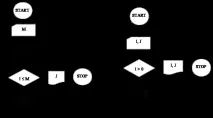
6. За програми, чиито блок-схеми са показани на фиг. 2.7–2.8, определете при какви стойности на данните ще приключи програмата. Намерете тези стойности и за случаите, когато:
а) на фиг. 2.7 проверкаI£Mзаменена сI£M;
б) на фиг. 2.8 командаI←I+ 1 се заменя сI←I+ 2;