Параметрични уравнения - Studiopedia
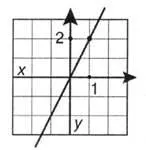
Кривите могат да бъдат представени аналитично, т.е. като графика на функция и графично. Математиците пишат това като: y = f(x), което означава, че "y е функция, чиято стойност зависи от стойността на x. Например най-простата функция y \u003d 2x означава проста зависимост: всяка стойност на y е два пъти всяка стойност на x. Графиката на тази функция е права линия, минаваща през началото (фиг. 1.1).
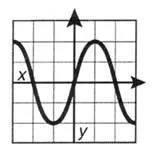
По-сложна форма са тригонометричните функции, например синусоида: y \u003d sin x
Графиката на такава крива е известна на всички (фиг. 1.2).
Този начин за представяне на функция и нейната графика се нарича явен. Това прави диаграмите относително лесни. Този метод обаче има значителни недостатъци по отношение на графичното представяне.
- Всяка стойностx съответства само на една стойностy. Това прави невъзможно започването на нова част от кривата на произволно място.
- Кривата не може да бъде затворена.
В резултат на това методът на явно представяне не може да се използва, когато се изисква описание на произволни криви, поставени на произволни места в равнината.
Алтернативен начин е да се дефинира кривата като параметрична функция.
По този начин и двете координати (x и y) са равни, т.е. и двете координати се изчисляват като функции на някакъв спомагателен параметър, често означаван със символа t. Най-общо подобна зависимост приема формата:
където x(t) и y(t) са функции на параметъра t.
Като се имат предвид същите стойности на t, функцията x(t) изчислява стойностите на координатата x, а функцията y(t) изчислява стойностите на координатата y. Това е много важна характеристика на работата.функции.
Познат пример. Можем да си представим, че стойностите на параметъра t са отброени времена, през които дадена частица се движи по произволна крива, като например кръг. Параметричната функция q(t) ще ви позволи да получите двойки координати, по които се движи точката в различни моменти (стойности) от времето t. Въпреки че в общия случай не е необходимо параметърът t да се свързва с времето.
Второто важно качество на параметричните криви е, че те имат по-разнообразни форми, отколкото позволяват изричните уравнения.
Друг пример. Графиките на синус и косинус не затварят изрично линията и две параметрични функции
y(t)= синт
създайте кръг, ако t "се движи" между 0 и 360 градуса.
Помощ. Параметричното представяне на функция е израз на функционална връзка между няколко променливи чрез въвеждане на спомагателни променливи, които обикновено се наричат "параметри". Ако имаме две променливи, например по оста x и по оста y, тогава връзката между тях може да се разглежда като уравнение на равнинна крива. Например, координатите x и y на точките на тази крива се определят от някакъв параметър, да речем, стойността на t, която се определя като определен диапазон от непрекъснати или дискретни стойности. Това представяне е особено важно за пространствени криви, тъй като предоставя по-лесен начин за чертане.
Използването на параметрични функции прави възможно използването на по-сложни функции от просто линейна апроксимация, тъй като един от основните недостатъци на апроксимацията с права линия е образуването на ъгли, които не създават впечатление за гладкост. Следователно неизбежната подмяна на прави сегменти можеда бъдат само криви, които са в състояние да осигурят необходимата гладкост (гледайки напред, можем да кажем, че говорим за криви на Безие и NURBS криви, които най-често се използват в компютърната графика). Но първо, нека дефинираме по-точно понятието гладкост.
Не намерихте това, което търсихте? Използвайте търсачката:
Деактивирайте adBlock! и обновете страницата (F5)наистина е необходимо