PhysicExperts, Сферични огледала
От всички неравнинни огледала ще разгледаме само сферичните, чиято отразяваща повърхност е външната или вътрешната част на сферата. Имаме вдлъбнато огледало (фиг. 6). Средата C на огледалото се нарича полюс.
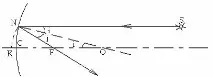
Всеки лъч, паднал върху огледалото през центъра на сферата (ъгълът на падане е нула), отразен, ще отиде в същата посока. Има само една точка O, която удовлетворява това условие. Нарича се оптичен център на огледалото. Всички прави, минаващи през оптичния център, са оптичните оси на огледалото. Една от оптичните оси минава през полюса C на огледалото, това е главната оптична ос. Останалите оптични оси са вторични.
Нека лъч, успореден на главната оптична ос, пада върху огледалото в точка N. NO е радиусът и следователно е перпендикулярен на сферата. Като построим ъгъла на отражение, равен на ъгъла на падане, получаваме отразения лъч NF. Ъглите на падане i и NOF са равни, тъй като вътрешните напречно лежат на успоредни прави и секуща. Следователно триъгълникът NOF е равнобедрен и ׀NF׀=׀FO׀.
Начертайте дъга NK с радиус FN. Пресечната точка на дъгата с главната оптична ос не съвпада с точка C, но е близо до нея. Отсечката ׀SK׀ е толкова по-малка, колкото SN е по-близо до главната оптична ос. Ограничаваме се до параксиални (параксиални) греди, така че можем да считаме сегмента ׀CK׀«׀CF׀ за пренебрежимо малък. За такива лъчи ׀CF׀=׀NF׀=׀FO׀, а точката F за всички параксиални лъчи лежи в средата на радиуса CO. Тази точка се нарича главен фокус на огледалото (разбира се, има фокуси по всички останали оптични оси - вторични). И така, основният фокус на вдлъбнато огледало е точката, в която след отражение се пресичат всички параксиални лъчи, падащи успоредно на главната оптична ос.
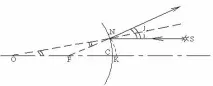
Подобни аргументи и конструкции ще ни доведат до концепцията за въображаемотоосновният фокус на изпъкналото огледало (фиг. 7). Разстоянието от огледалото до главния фокус се нарича фокусно разстояние и се обозначава с F. Може да се докаже, че всички лъчи, падащи от една точка, след отражение от вдлъбнато огледало, преминават през една точка - изображението (това може да се докаже поне чрез конструкция; поради приближаването на условието за параксиалност, това, разбира се, не е съвсем точка, а малко петно, за изпъкнало огледало - това е точката на пресичане на продължението на всички отразени лъчи ). За да се построи такава точка, са достатъчни всеки два лъча. Лъч, падащ успоредно на главната оптична ос, след отражение ще премине през главния фокус (или продължението на отразения лъч ще премине през главния фокус - за изпъкнало огледало). Според закона за обратимостта лъчът, падащ през главния фокус, след отражение ще премине успоредно на главната оптична ос. И накрая, лъч, падащ през центъра на сферата, ще се отрази в същата посока.
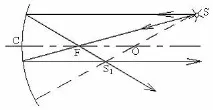
При конструиране на изображение точките във вдлъбнато огледало (фиг. 8) маркират точки O, F, C, след което се изграждат всеки два от трите изброени лъча. Всички други отразени лъчи също ще преминат през точката на пресичане на отразените лъчи S1 - това е реалният образ на точката S. Конструкцията на изображението в изпъкнало огледало е подобна.
Нека изградим изображение на обект AB във вдлъбнато огледало (фиг. 9). Изображение A1 се намира, както на фиг. 8. Изграждането на изображението на точка, разположена на главната оптична ос, се извършва по следния начин: изчертаваме произволен лъч VM и успоредно на него съответната странична ос OD; в средата на разстоянието OD има страничен фокус F1, през който ще премине отразеният от точката M лъч. Като втори лъч е удобно да изберете лъч, преминаващ по главната оптична ос. Пресечна точка на два отразени лъча - изображениеВ 1.
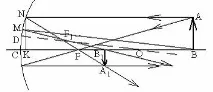
Нека означим разстоянието от огледалото до обекта d=׀CB׀; разстояние от огледалото до изображението f=СB1; фокусно разстояние F=׀CF׀≈׀KF׀. От подобието на триъгълници А1В1F и NKF следва равенството
аналогично, от подобието на триъгълници A1B1O и ABO