Постановка на проблема за оптималното портфолио - Studiopedia

В литературата са описани различни подходи за формиране на оптимално портфолио с помощта на моделите на Блек, Марковиц, Тобин.

Проблемът с оптимизацията се свежда до определяне на такава структура на инвестиционния портфейл, така че размерът на очаквания доход и нивото на риск да съответстват на целите на инвеститорите. В този случай целевата функция може да бъде минимизиране на риска за дадена доходност или максимизиране на дохода за риск не по-висок от даден. Могат да бъдат наложени различни ограничения върху компонентите на вектораХ, който представлява състава на портфейла, в зависимост от вида на сделката, вида на участващите активи, размера на отворените позиции и т.н. Портфейли, които отговарят на условията на този пазар, се наричат допустими.

1) В черния модел са допустими всякакви портфейли, т.е. векторXудовлетворява само основното ограничение:

. (4.6)

Наличието на къси позиции (липса на условието за неотрицателност) ви позволява да реализирате произволно голяма доходност, естествено за сметка на висок риск.

2) Моделът на Марковиц счита само стандартни портфейли за валидни (без къси позиции). Това означава, че на вектораХса наложени две ограничения: главното и неотрицателносттаxi ³ 0за всичкиi.

Портфолиото се нарича стандартно, ако инвеститорът е в дълга (long) позиция за всеки актив.

Дълга позиция -обикновено е закупуване на актив с намерение за последваща продажба (затваряне на позиции). Такава покупка обикновено се прави в очакване на увеличение на цената на даден актив с надеждата да се спечели от разликата между покупната и продажната цена. Ако инвеститорът е сигурен в обратното по отношение на даден актив, тоест в намаляване на стойността му, тогава той може да сключи сделка,което се нарича "къса продажба" (къса продажба). За да направи това, той взема този актив назаем от друг инвеститор (заемодател), незабавно го продава и впоследствие го купува на пазара на намалена цена и го връща на своя заемодател. В същото време той е длъжен да плати на кредитора текущия доход от актива по време на сделката и определен процент за осигуряване на самата възможност за сделката (за заема). На повечето фондови борси късите продажби са доста приемливи и често използвани, но поради особения си риск борсите могат да наложат ограничения върху общия размер на късите позиции в транзакциите.

В модела на Марковиц обикновено се разглеждат два вида проблеми за оптимизиране на портфейла: минимален риск за дадено ниво на възвръщаемост и максимална ефективност за ниво на риск, което не надвишава дадена стойност.

Марковиц портфолио с минимален риск. Изложението на този проблем може да се тълкува по следния начин. Намерете вектораX* разпределението на първоначалния капитал, минимизирайки риска (вариацията) на портфейла

(4,7)

за дадена ефективност на портфейла

,(4.8)

и условието, че сумата от дяловете на активите в портфейла трябва да бъде единица

Тук ковариационната матрица еi j =.

Пример 4.2. Формирайте портфейл с минимален рискspот два вида ценни книжа А с ефективност 12% и риск 21,2 и Б с ефективност 5,1% и риск 8,3, при условие че доходността на портфейла (mp =S xi mi)е не по-малка от 8,9%. Двойният корелационен коефициент между тези ценни книжа е 0,18.

1. Да въведем обозначението:x1 - дял в портфейла от ценни книжа А; x2 - дял в портфейл B,

2. Нека формулираме проблема за формиране на оптимален портфейл според модела на Марковиц, като вземем предвид първоначалните данни.

Необходимо е да се намери векторX*= (x1,x2), който минимизира риска на портфейла:

sp= ==

= ®мин,

със следните ограничения:

Този проблем е сведен до квадратичен програмен проблем.

3. Решението на горния проблем може да се извърши чрез графичен метод или с помощта на добавката в Excel Find a solution.

Графична илюстрация на решението на задачата е показана на фиг. 4.5.

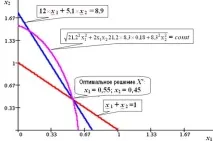
Ориз. 4.5. Минималният портфейлен риск, равен на 12.88, се достига в точката на пресичане на три линии (x1=0.55 иx2=0.45), съответстващи на ограниченията 12´x1 + 5.1´x2³8.9 иx1 +x2 = 1 и целевата функция

За решаване с помощта на добавката Търсене на решение първо се съставя стандартен формуляр на Excel лист за решаване на оптимизационни проблеми, като се използва добавката Търсене на решение, както е показано на фиг. 4.6. След това директно се използва добавката Търсене на решение.

Ориз. 4.6. Изходни данни и формули за изчисление

Резултатите от изчисляването на състава на оптималния портфейл според критерия за минимален риск са показани на фиг. 4.7.

Фиг.4.7. Резултати от изчисляването на състава на оптималния портфейл

В клетка E5 се получава минималната стойност на целевата функцияσp= 12.880, а в клетки B4:C4 са записани стойноститеx1 = 0.551 иx2 = 0.449 - съответно акции от тип A и тип B. В същото време посочените ограничения са напълно изпълнени, ефективността на портфейла е 8,9% (клетка G8).

Пример 4.3. Формирайте минимален рисков портфейл от три ценни книжа A, B и C (характеристиките на ценните книжа са дадени в таблицата), осигурявайки

Индекс	Тип сигурност
А	б	° С
Ефективност,mi, %	5.1	9.5
Риск,σi	21.2	8.3	14.5

които осигуряват средна възвръщаемост на портфейлаmpот поне 12,5%. Матрицата на двойните коефициенти на корелация между ценните книжа е известна:

1. Да въведем обозначението:x1,x2,x3 – съответните дялове на ценни книжа A, B и C в портфейла.

2. Нека запишем икономико-математическия модел (EMM) на проблема за формиране на оптималния портфейл според модела на Марковиц в общ вид:

3. Да подготвим лист за решаване на задачата, фиг. 4.8. и тук първо формираме ковариационната матрица (клетки F17:H19), чиито елементи се изчисляват чрез израз (4.5).

Ориз. 4.8. Excel лист с изходни данни и изчислителни формули за изчисляване на състава на оптималния портфейл от три ценни книжа

4. Нека напишем проблема EMM в разширена форма, като вземем предвид началните условия и изчислената ковариационна матрица:

5. В резултат на решаването на задачата клетките (B5:D5) ще съдържат елементи от оптималния векторХ*= (0,23; 0,27; 0,50), минимизиращ риска на портфейла, който е σp = 1,01 (клетка G6) и осигурява ефективността му от 8,9% (клетка E8), фиг. 4.9.

Ориз. 4.9. Excel лист с резултатите от изчисляването на състава на оптималния портфейл от три ценни книжа

Портфолио на Марковиц с максимална ефективност.Намерете вектораX* максимизиране на очакваната ефективност на портфолиото

=> макс.(4,10)

при ниво на риск, което не надвишава предварително определена стойност

, (4.11)

и условието, че сумата от дяловете на активите в портфейла трябва да бъде единица

Ако в оптималното решение стойноститеxi *³ 0, тогавапрепоръчително е да инвестирате дялxi *от паричния капитал в ценни книжаi-ти тип. Акоxi ** ³ 0. Вместо операцията „къса продажба“, инвеститорът може да използва пари в брой при безрискова ставка.

Характеристика на модела на Марковиц е, че възвръщаемостта на всеки стандартен портфейл не надвишава най-високата възвръщаемост на активите, от които е изграден.

Пример 4.4 Намерете оптималния портфейл с максимална ефективност за три ценни книжа R, S и L с известна доходностmiи риск σi(виж таблицата):

Р	С	Л
мили (%)	10.5
си

Коефициентите на корелация на двойки между ценните книжа са представени под формата на матрица:

Р	С	Л
Р	0,52	0,27
С	0,52	0,75
Л	0,27	0,75

Горната граница на риска σpне трябва да надвишава 16.

1. Да въведем обозначението:x1,x2,x3 – съответните дялове на ценни книжа R, S и L в портфейла.

2. Нека запишем EMM на проблема за формиране на оптималния портфейл според модела на Марковиц в общ вид:

σp ,

3. Нека формулираме проблемите на EMM, като вземем предвид конкретни първоначални данни. Намерете вектора X= (x1,x2,x3), който максимизира възвръщаемостта на портфейлаmp.

при следните ограничения

sp = 16

COV=

За решаване на проблема се използва EXCEL добавката Търсене на решение. Първоначалните данни и формулите за изчисление са представени на фиг. 4.10.

Ориз. 4.10. Фрагмент от Excel лист с изходни данни и изчислени

В резултат на решението беше получена максималната възможна възвръщаемост на портфейла от 11.32 със стойностите на вектора X, записани в клетки $B5:$D5 (фиг. 4.11.)

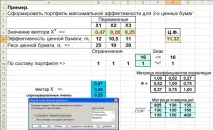
Ориз. 4.11. Фрагмент от Excel лист с резултатите от изчисляването на оптималния портфейл

Отговор: Максималната доходност от 11,29% може да се получи, ако дяловете на акциите R, S и L са 0,47, 0,28 и 0,25.

Не намерихте това, което търсихте? Използвайте търсачката:

Деактивирайте adBlock! и обновете страницата (F5)наистина е необходимо