Примери за интерполация на функции
Примери за интерполация на функции
Въпреки очевидната простота на формулите за интерполация, тяхното изпълнение под формата на програмни блокове е доста тромаво. Нека дадем примери за най-простите варианти на програмни блокове, които описват интерполационни функции, използвайки разглежданите методи. В нашите примери x, y са вектори на таблични стойности на аргумента и функцията (възли); xf е стойността на аргумента, при който трябва да се изчисли стойността на функцията.
1. Формулата за линейна интерполация се прилага към двойката възли, между които се намира стойността на аргумента, следователно в представения блок възлите се преобръщат, за да се определи желаната двойка:
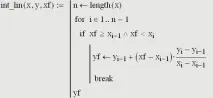
2. Проблемно е формулата за интерполация на Лагранж да се напише директно в математически символи поради сложността на изчисляването на продуктите (и в двата случая се изключва един фактор), поради което се предлага следният програмен блок:
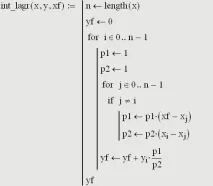
3. Mathcad има вградена функция linterp(vx, vy, x), която връща стойността на функцията в точка x, изчислена чрез линейна интерполация на данни с точки, чиито координати се съхраняват във векторите vx и vy.
Моля, имайте предвид, че резултатите от интерполацията в примери 1 и 3 са напълно еднакви, тъй като те използват един и същ метод за решаване на проблема, точността на изчисляване на стойностите на функцията с помощта на формулата на Лагранж е по-висока.
Нека илюстрираме последното твърдение с графика, на която възлите на функцията са дадени с точки (7 точки от синусоидата на интервала [0, 2π]), синьото е резултат от линейна интерполация, а лилавото е интерполация по формулата на Лагранж.
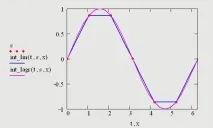
Очевидно последният резултат е най-добрият.
4. Последният пример в този раздел демонстрира използването на интерполация при интегриране на таблично дефинирана функция. Имайте предвид, че ако използвате интерполация за изчисляванеинтегранд или неговите компоненти, тогава става възможно да се оцени определен интеграл с граници на интегриране, които не съвпадат с възлите, и за произволен брой стъпки на интегриране, т.е. да се увеличи точността на изчисляване на интеграла. В този случай е препоръчително да се използват нелинейни методи за интерполация, например формулата на Лагранж, разгледана тук.