Проективна геометрия Дефиниция на хомоложни елементи в проективни снопове - PIZiadas GRÁFICAS
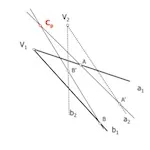
За по-нататъшно изследване на методологията, която ще се използва, ще се използва модел с двоен елемент, базиран на „артикули“, т.е. с права линия, като освен това се приема, че основите на съответните греди са разделени.
Затова ще разгледаме дефиницията на хомоложни елементи в две проективни, които нямат общи елементи. Изложението на проблема като цяло може да бъде:
Дадени са два проективни снопа, дефинирани от три двойки елементи на (директния) двойник, дефинирайте аналог на дадения лъч.
Тези мълнии могат да принадлежат към всяка една от гредите и затова ние търсим да принадлежат към основата на другата.
Ние решаваме този проблем, като използваме междинни перспективи, зададени между два проективни снопа, като по този начин получавамепроективния център на двата снопа (точкаCp ). Както видяхме, проективният център на сноповете е перспективният център на серията, която получаваме, за да прережем гредите на снопа към всеки друг елемент и едновременно с това да разделим техните двойници от двойника на геометричния елемент, използван като основа в първата секция.
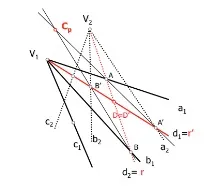
Проективни централни два лъча (Централен перспективен ред)
Така или иначе щедефинираме, така чепроективният център е два лъча.
Получаване на проективния център на два лъча:
Различните случаи, които могат да възникнат, ще се определят от данните, определящи проективните пакети, по принцип могат да бъдат:
- Двойка прости колеги от лъча (3максимум)
- Конвенционални рентгенови колеги в бази (макс. 2)
- Локус, където оста е проективна
Можем да комбинираме тези данни, за да идентифицираме конкретен проблем, когато внесем необходимото количество от тях. Проблемът ще бъде дефиниран, когато знаем три двойки хомоложни елементи или еквивалентни данни. И така, решете този първи случай:
Дадени са три прави (лъчеви) снопове и техните хомолози, определете проективния център на посочените греди
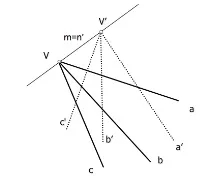
Тези линии на данни k, b y c (лъч на светлинен връх V), както и съответните им аналози лъчи ", B' y c '. Основите на общия лъч t = n' съдържат линия за всеки от лъчите.
За да се определи дали проективният център се нуждае от няколко реда, които го съдържат. Това може да се дефинира като проекция на две хомоложни точки в две гледни точки на серия основа на двойка хомоложни лъчи.
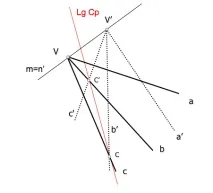
Локус на проективния център
Полученият локус може да се разглежда като проекция на лъч на две хомоложни последователности от точки, получени чрез разделяне на секции от BYB 'B и B' лъчи, но също така разбираме, че основата на серията е sus' и секционни лъчи B и B'.
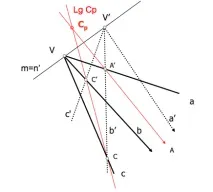
Центърът се определя от пресичането на място, което е намерено преди това, и друго, което се получава подобно на предишното, b лъчи се докосват с техните двойници 'y b', за да дадат точки A и A' перспективна серия.
Хомоложните лъчи, съдържащи основите, са линиите, които излизат от проективния център от всяка от основите (върховете на лъчите). Тези елементи могат да бъдат получени като аналог на всеки неизвестен лъчX илигодина’.
Получаване на подобни артикули
С помощта на проективния център е лесно да се идентифицира аналогът на всеки лъч; Пример е аналог на точката X.
За опростяване на фигуратаоставаме с елемент a и неговия колега
близо до центъра Проективни снопове.
Ако срежем по линията x, се генерира точка (') и нейният двойник (гръбнакът на серията) ще се окаже на линия с проективния център. Елементът на хомоложна точка (A) съдържа (x') търсете.
Да завърши проучването на други изучени примери, които затвърждават предложените концепции.
Определете проективния център на гредите и хомолога на един от лъчите в следните случаи: