Равнинна апроксимация

Вижте също:

1. Апроксимация чрез сплайни.
2. Нелинейна апроксимация с полином от 2-ри ред.
3. Пресечна точка на повърхнина с равнина. Тела с изрези
4. Пресечна точка на права с равнина. Условието за принадлежност към права равнина
5. Апроксимация (апроксимация) на функции (хармоничен анализ).
6. Ъгълът между права и равнина.

Множествена регресия.

В Matkad е възможно да се приложи множествена регресия, като се използват вградени функции само за два аргумента. Множествена регресия с повече от тях може да бъде реализирана с помощта на функциятаminerr (минимална грешка).

Множествената регресия на два аргумента е реализирана в Matkad с помощта на функциятаregress( M, vz, n)

Функциятаregress връща координатите на апроксимиращата повърхност.

Тук M е 2*m матрица от две колони и m реда, в които се въвеждат наблюдаваните данни на два аргумента, vz е векторът на наблюдаваните стойности на апроксимираната функция,

n е степента на апроксимиращия полином. За n=1 имаме линейна, за n> 1 - нелинейна множествена регресия.

Матрицата на аргументите M и векторът на наблюденията vz са дадени (вижте фигура 4). Векторът vs определя коефициентите на апроксимиращата равнина. Тук долният елемент е коефициентът при x, следващият е коефициентът при y, а третият отдолу е свободният член.

Фиг.4. Изчисляване на първоначалните данни на вектор vs

Съставяме уравнението на равнината

Сега, както винаги, когато формираме триизмерна графика, създаваме матрица за вземане на решения и изграждаме графика или (и) получаваме таблица с решения в възловите точки.

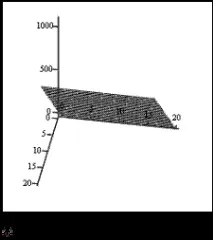
Фиг.5. Диаграма на линейна множествена регресия.

---