Report2logis (1)

Министерство на образованието и науката на България

Федерална държавна бюджетна образователна институция за висше професионално образование

„САМАРСКИ ДЪРЖАВЕН Аерокосмически

УНИВЕРСИТЕТ на името на академик S.P. КРАЛИЦА

Национален изследователски университет (SSAU)

Факултет по икономика и управление

Лабораторен доклад #2

"Прилагане на математически модел на транспортна задача за съставяне на оптимален транспортен план"

курс: Логистика

Изпълни: Василенкова А.С., гр. 742

Проверен: Просвиркин Н.Ю.

Първоначалните данни на проблема са обемите на очаквания транспорт на ресурси от доставчици до потребители, разходите за тяхната доставка.

Имаmдоставчици (i=1,m), които имат наличност от определен продукт в размер наaiединици, съответно, иnпотребители (j=1,n), които имат нужда от продукта в обеми отbjтоварни единици, съответно. Известни са транспортните разходи за транспортиране на единица продукт от точките на доставка до дестинацииcij– транспортни разходи за транспортиране на единица товар от i-тия доставчик до j-тия потребител. Чрезxijще обозначи броя на единиците продукти, транспортирани по маршрута (i, j). В заключение ще се определи стойността на целевата функция F, която характеризира размера на общите транспортни разходи.

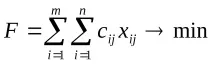
1.2 Постановка на проблема:

Въз основа на първоначалните данни, като използвате известни методи (ъгъл „северозапад“, минимална цена, метод на Vogel), намерете първоначалния осъществим транспортен план, проверете неговата оптималност, като използвате потенциалния метод и, ако е необходимо,извършете една стъпка за оптимизация.

Намерете оптималното решение с помощта на добавката Ms Excel „Търсене на решение“ за транспортен проблем с допълнителни условия:

- Фиксирано захранване от i-тия доставчик до j-тия потребител;

- Доставки с ограничения в обема на превозваните стоки.

Въз основа на резултатите от търсенето на оптималното решение на основната версия на задачата се задават допълнителни ограничения.

1.3 Алгоритъм за решаване на транспортната задача:

1. проверка на близостта на транспортната задача

2. намиране на референтен план (решение, основа)

- Метод на северозападния ъгъл

- метод на "минимални разходи"

3. проверка на основния план за оптималност

4. преход от един основен план към друг до търсене на оптималното решение

2.1 Решаване на транспортния проблем с помощта на метода на северозападния ъгъл

При този метод дистрибуцията на продуктите се извършва по дестинации според приоритетите. Намаляването на приоритета става в посока отгоре надолу и отляво надясно, т.е. на първо място се запълват тези маршрути, чиито доставчици и потребители са разположени в горния ляв ъгъл на матрицата (северозападен ъгъл). След това последователно се запълват останалите елементи на матрицата. За тази цел е разработен следният алгоритъм.

Всеки xij е избран за ролята на първата основна променлива в общата настройка и се приема, че xij – min(bj ai)/

В този случай стойността на целевата функция не се анализира. На първо място, този метод е предназначен да намери възможни решения, които съответстват на системата от ограничения.

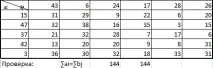
В хода на решаването на проблема бяха получени следните стойности:

2.2 Решение на транспортния проблем по метода на "минималните разходи"

Методминималните разходи включват следната последователност от действия. В тарифната таблица най-малката стойност се избира от всички стойности на разходите и в клетката (i, j). с най-малка цена се записва min(ai bj), тоест най-малкото от числата ai и bj. Ред i се изключва от по-нататъшно разглеждане, ако запасът ai е напълно експортиран, или колона j, ако търсенето bj е напълно удовлетворено, или ред и колона, ако ai=bj. Сред останалите клетки отново се запълва клетката с най-ниска цена и така нататък, докато се изпълнят всички ограничения на проблема и се намери референтно решение.

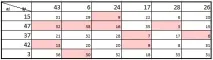
Решение на транспортния проблем по метода на Фогел

Методът на Фогел е постепенно попълване на клетките на таблицата. На първия етап се намира разликата между най-ниските транспортни разходи във всеки ред и всяка колона на таблицата. Тези разлики се въвеждат в съответния допълнителен ред и колона на таблицата. След това се избира редът (колоната) с най-голямата стойност на разликата и стойността min(ai bj) се записва в клетката с най-малката цена, съответният ред или колона се зачертава, както при метода на минималната цена. На следващия етап за останалите клетки отново се намира редът или колоната с най-големите стойности на разликите на минималните стойности на разходите и така нататък, докато се намери референтно решение. Този метод ви позволява да намерите референтен план, близък до оптималния.

3. Метод на потенциалите (за базовия план, получен по метода на "минималните разходи")

Алгоритъм за решаване на проблема въз основа на потенциалния метод:

Потенциалите на доставчиците ui(i=1,m) и vj(j=1,n) се намират от стойностите cij в попълнените (xij>0) клетки на таблицата. Тъй като m + n-1 клетки от таблицата са попълнени в основния план,тогава за определяне на потенциалите е необходимо да се състави система от m+n-1 линейно независими уравнения, където v=u-c. Такава система е неопределена, така че на едно неизвестно се дава нулева стойност (u1=0).

Намират се стойностите на характеристиките на свободните (xij=0) клетки на таблицата.Ако за всички свободни клетки>0, тогава основният план е оптимален. Ако има стойности за съседни файлове в Отговорите на теста за маркетинг

#

---