Решаване на линейни системи от уравнения с директни и итеративни решения, блог на COMSOL
Решаване на линейни системи от уравнения: директни и итеративни решения
 Уолтър Фрай 11/11/2013
Уолтър Фрай 11/11/2013

В тази публикация в блога ще представим два класа алгоритми, които се използват в COMSOL за решаване на системи от линейни уравнения, които възникват при решаването на всеки проблем с крайни елементи. Такава информация е от съществено значение за разбирането както на вътрешните алгоритми на решаващия (компютърната програма), така и на нарастващите изисквания към паметта поради количественото усложняване на проблема.
Линеен статичен проблем с крайни елементи
Помислете за линеен статичен проблем с крайни елементи, съставен от три възела и три елемента:
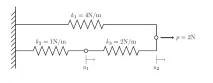
Всеки елемент е ограничен от два възела. Един от възлите е разположен на твърда стена, където, както е известно, преместването е нула и не е необходимо да се решава уравнението за този възел. Точно както в предишната публикация в блога за линейни статични проблеми с крайни елементи, можем да запишем уравненията за баланс на силата за всеки възел:
можете също да ги напишете във формата:
или дори в по-компактна форма:
Можем да решим този проблем с помощта на итеративния метод на Нютон-Рафсън и тъй като проблемът е линеен и статичен с начална стойност \mathbf_=\mathbf, решението ще бъде намерено в една итерация:
Освен това в този проблем има само две неизвестни или степени на свобода (DOF) и може лесно да се реши с химикал и хартия. Но като цяло вашите матрици ще бъдат от хиляди до милиони DOF и намирането на решението на горното матрично уравнение е най-изчислителната част от проблема. Когато решавате такива системи от линейни уравнения на компютър, трябва да имате и концепцията заномерът на условието, мярката за чувствителността на решението към промяна във входните данни. Въпреки че в средата COMSOL числото на условието никога не се изчислява директно (тъй като е сравнимо по време с решаването на самия проблем), ние ще говорим за него в относителни термини. Това число играе важна роля в числените методи, използвани при решаването на системи от линейни уравнения.
Има два основни (фундаментални) класа алгоритми, използвани за решаване на \bfb> : директни и итеративни методи. Ще представим и двете групи от тези методи и ще разгледаме техните общи свойства и относителна ефективност по-долу.
Директни методи
Решавателите с директен метод, използвани в COMSOL, са решателите MUMPS, PARDISO и SPOOLES. Всички те използват метода на LU факторизация, наричан още LU факторизация.
Всички тези програми за решаване дават едно и също решение за всички добре поставени проблеми с крайни елементи, в които имат най-голямо предимство. Те дори могат да решат някои неправилни задачи. От гледна точка на решение, няма значение кой решаващ инструмент ще изберете, тъй като всички те ще намерят едно и също решение. Директните решаващи програми се различават само по относителната си скорост на изпълнение. Всеки от решаващите програми MUMPS, PARDISO и SPOOLES може да се възползва от всички процесорни ядра на една и съща машина, но PARDISO ще бъде малко по-бърз, а SPOOLES малко по-бавен от другите директни решаващи програми. SPOOLES обаче използва най-малко памет. Всички директни решаващи програми изискват много RAM, но MUMPS и PARDISO могат да съхраняват решението извън ядрото, което означава, че могат да използват твърдия диск за решаване на някои проблеми (създаване на файл за пейджинг). Решавателят MUMPS също поддържа клъстерни изчисления, което позволяваизползват повече памет, отколкото предоставя една машина.
Ако решавате проблем, който няма решение (например структурен проблем с неограничен товар), директните решаващи програми пак ще се опитат да разрешат проблема, но най-вероятно ще върнат съобщение за грешка като това:
Ако получите този тип съобщение за грешка, тогава трябва да проверите отново всичко, за да сте сигурни, че задачата е зададена правилно.
Итеративни методи
Итеративните решаващи програми в COMSOL покриват много различни подходи, но всички те са концептуално достатъчно прости за разбиране, като по същество са подобни на метода на конюгирания градиент. Други методи включват метода на обобщения минимален остатък и метода на стабилизирания биконюгатен градиент и много техни варианти, но всички те се държат по подобен начин.
За разлика от директните решаващи средства, итеративните методи подхождат към решението постепенно, в повече от една изчислителна стъпка. Следователно при решаване на проблема по итеративен начин може да се наблюдава намаляване на оценената грешка на решението с увеличаване на броя на повторенията. За добре обусловени проблеми сходимостта ще бъде равномерно монотонна. Ако имате работа с проблем, който не е (достатъчно) добре обусловен, тогава конвергенцията ще бъде по-бавна. Осцилаторното поведение на итеративния решаващ инструмент често сигнализира, че проблемът не е добре дефиниран, например когато проблемът не е достатъчно ограничен. Типичен график на конвергенция за итеративен решаващ инструмент е показан на фигурата по-долу:
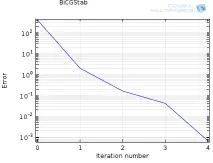
По подразбиране моделът се счита за конвергиран, когато резултатът за грешка (решение) в итеративния решаващ инструмент стане по-малък от 10 -3 . Тази настройка се контролира в прозорецаНастройки на Solver:
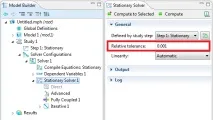
Голямо предимство на итеративните методи е тяхната употреба на памет, която е много по-малка от тази на директните решаващи задачи при решаване на проблеми с една и съща величина (брой уравнения). Значителен недостатък е, че итеративните решаващи програми не винаги „просто работят“. Различната физика изисква различни итеративни настройки за решаване в зависимост от естеството на уравненията, които се решават.
За щастие, COMSOL вече идва с вградени настройки по подразбиране за решаване на всеки проблем от физиката. COMSOL автоматично ще определи частта от физиката на проблема, който се решава, както и неговия размер и ще избере програма за решаване - директна или итеративна - за този случай. По подразбиране итеративните решаващи програми се избират въз основа на изискванията за най-добра точност и най-малко използване на паметта и не изискват намеса на потребителя за настройката им.
Ключови констатации за директни и итеративни методи за решаване
За решаване на системи от линейни уравнения, които възникват по време на симулация, COMSOL автоматично ще избере най-добрия инструмент за решаване без намесата на потребителя. Директните решаващи програми използват повече памет от итеративните решаващи, но в същото време имат по-голяма точност (за добре поставени проблеми). Итеративните решаващи програми се доближават до решението постепенно и можете да промените относителната грешка на решението по желание.