Решаване на транспортната задача по потенциалния метод в Excel с пример
Нека решим транспортната задача по метода на потенциалите. Ние познаваме наличностите за продажби, заявките на клиентите и разходите за доставка на единица. Нека направим три начални таблици.
Нека изградим основен план на транспортната задача с помощта на инструмента "Търсене на решения". След това ще съставим таблици с еднакъв размер с празни клетки. Таблица А е аналог на таблицата на разходите, B - "резерви", C - "търсене".
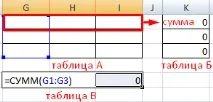
Елементите на таблица B са сумата от съответните редове в таблица A. Елементите на таблица C са сумата от съответните колони в таблица A.
Отделно ще съставим получената таблица D. Тя ще отразява оптималните транспортни разходи. Всеки елемент от таблица G е произведението на елемент А и съответния елемент от таблицата на разходите.
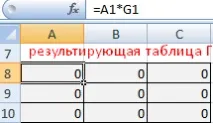
На отделно място на листа въведете формулата на функцията: =SUMPRODUCT(A1:C3;G1:I3)
Първият масив е таблицата с разходите, вторият е диапазон A.
Поставяме курсора в клетката със стойността на функцията. Наричаме инструмента „Търсене на решение“. Попълване на диалоговия прозорец:
В отворения диалогов прозорец щракнете върху бутона "Опции" и задайте следните настройки:
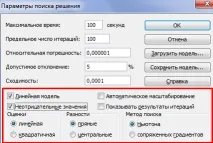
Щракнете върху OK - Изпълнение. Получаваме основния план на транспортната задача:
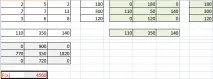
Изпълнен е с бледозелен цвят. Клетките със стойности над нулата се наричат "основни", "заети". Клетките със стойност 0 са "свободни".
Продължаваме по план:
Нека преброим броя на заетите клетки с помощта на функцията COUNTIF.
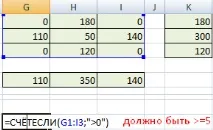
Тъй като резултатът е 5, основният дизайн не е изроден. Да проверим оптималността на референтния план - да намерим потенциалите за заетите клетки.
Трябва да създадете система от уравнения. Приема се, че αj = 0, а αi + βj = сij (разходи за доставка на единица товар). Извикваме командата "Търсене на решение". Ние създаваме условиясистеми от уравнения като ограничения.
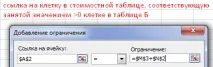
Завършен диалогов прозорец:
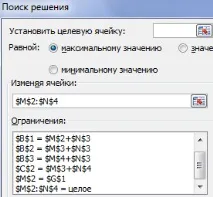
Резултатът от инструмента "Търсене на решение":
Нека изчислим оценките на свободните клетки. Формула: cij - (αi + βj). Взимаме свободна клетка от таблица A. Гледаме нейната стойност в таблицата с разходите. Това ще бъде cij. След това разглеждаме какви потенциали съответстват на тази клетка. Вмъкваме техните стойности във формулата.
В Excel намираме оценки с помощта на математически оператори и връзки към съответните клетки.
Планът се счита за оптимален, ако оценките са по-големи или равни на 0. В нашия случай имаме отрицателни стойности - планът не е оптимален. Затова продължаваме напред.
Намираме коя клетка в таблица А отговаря на минималния резултат. Изграждаме цикъл за тази клетка - затворена начупена линия. Условия: редуването на вертикални и хоризонтални посоки е задължително, само в основни клетки.
В оригиналната клетка (с минимален резултат) поставяме знака „+“. След това редувайте: "-", "+" и т.н.
В таблицата с разходите намираме минималната стойност със знак „-“.
В нашия пример това е "5", клетка B1. Тази клетка трябва да бъде премахната от основата. И направете клетката с минимален резултат основна.
Отчитайки променените данни, ние отново изграждаме основен план за транспортната задача. Използваме инструмента "Търсене на решение". Преизчисленият транспортен план изглежда така:
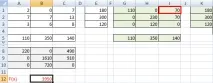
Моля, обърнете внимание: клетка I1 (където имаше минимален резултат) стана основната, заета.
Извършваме същите изчисления за новия план (от точка № 1): намираме потенциалите, оценките на свободните клетки, за да проверим оптималността. И така нататък, докато оценките на свободните клетки са по-големи или равни на 0.