Силно свързани компоненти - страница Михаил Медведев
Дефиниция. За насочен граф се казва, че е силно свързан, ако всеки друг връх е достижим от всеки връх (по насочени дъги).
Произволен насочен граф може да бъде разложен на силно свързани компоненти, които се дефинират като класове на еквивалентност "u достижимо отv иv достижимо отu ".
Теорема. Графът е силно свързан (т.е. състои се от един силно свързан компонент) тогава и само ако следните две условия са изпълнени за всеки връхv :
- от връхv всички други върхове на графа са достижими;
- връхv е достижим от всеки връх на графа;
Дефиниция. Силно свързан компонент на насочен графG(V, E) е максималният набор от върховеCV, така че за всяка двойка върховеu иv отC върховетеu иv са достижими един от друг.
Дефиниция. Транспонирането на графикаG(V, E) е графикаG T (V, E T ),
къдетоE T = u, v) : (v, u) E>.
ГрафитеG иG T имат еднакви силно свързани компоненти, тъй катоu иv са достижими един от друг вG тогава и само ако са достижими един от друг вG T.
Следният алгоритъмKosarayu намира силно свързани компоненти на насочена графикаG(V, E) в линейно времеO(V + E).
Силно свързани компоненти (G)
1. Извикваме първо търсене в дълбочинаDFS(G), изчисляваме терминиращи маркировкиf[v] за всеки връхvV.
2. Изграждаме транспонираната графаG T.
3. Извикваме първо търсене в дълбочинаDFS(G T ), но в главния цикъл на процедуратаDFS разгледайте върховете в низходящ ред наf[v] стойности.
4. Дърветата на гората за търсене в дълбочина, получени в стъпка 3, са силно свързани компоненти.
Въз основа на този алгоритъм, компонентната графикаG SCC (V SCC, E SCC) се определя, както следва. Нека графикатаG има силно свързани компонентиC1,C2, …,Ck. Наборът от върховеV SCC = v1, v2, …, vk> се състои от върховетеvi за всеки силно свързан компонентCi на графикатаG.
Пример. Разгледайте прилагането на алгоритъма за изчисляване на силно свързани компоненти, използвайки пример.
1. ИзвикайтеDFS(G), поставете етикетиd[v] / f[v] близо до всеки връхv :
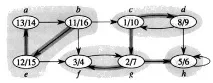
2. ИзчислетеG T :
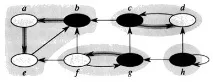
3. ИзвикайтеDFS(G T ), разглеждайки върховете в низходящ ред наf[v] стойности. Получаваме графиката на компонентите:
4. Силно свързаните компоненти в графиката ще бъдат:a, b, e>,c, d>,f, g> иh>.
Лема. НекаC1 иC2 са различни силно свързани компоненти в насочен графG(V, E). Некаu1,v1C1,u2,v2C2 и същоG имат пътu1u2. Тогава вG не може да има пътv2v1.
Доказателство. Ако приемем обратното, тогава върховетеu1 иu2 ще бъдат достижими един от друг (u2v2v1u1 ). Тоест тези върхове трябва да бъдат включени в един силно свързан компонент.
НекаUV. Нека дефинирамеd(U) =,f(U) =. Тоестd(U) иf(U) представляват най-ранното отворено време и най-късното крайно време за всички върхове отU.
Лема. НекаC1 иC2 саразлични силно свързани компоненти в насочен графG(V, E). Нека има ребро(u, v)E, къдетоuC1,vC2. Тогаваf(C1) >f(C2).
Проблем. За всеки силно свързан компонент изведете списъка с върхове, които съдържа.
Вход. Първият ред съдържа броя на върховетеn в графиката. Всеки следващ ред описва насочено ребро на графа и съдържа номерата на върховете, които свързва. Върховете на графа са номерирани от1 доn.
Изход. За всеки силно свързан компонент изведете неговия пореден номер, както и списъка с върховете, включени в него, във възходящ ред. Компонентите трябва да се извеждат в произволен ред.