Средни линии на геометрични фигури

Гомелска научно-практическа конференция на ученици по математика, нейните приложения и информационни технологии "Търсене"

1. Свойства на средните линии

2. Триъгълник, четириъгълник, успоредник

3. Четириъгълник, тетраедър. Центрове на масата

4. Тетраедър, октаедър, паралелепипед, куб

Списък на използваната литература

Геометрията е неразделна част от общата култура, а геометричните методи служат като инструмент за разбиране на света, допринасят за формирането на научни представи за околното пространство, разкриването на хармонията и съвършенството на Вселената. Геометрията започва с триъгълник. В продължение на две хилядолетия триъгълникът е бил сякаш символ на геометрията, но не е символ. Триъгълникът е атом на геометрията. Триъгълникът е неизчерпаем – непрекъснато се откриват нови негови свойства. За да говорите за всичките му известни свойства, ви е необходим том, сравним по обем с обема на Голямата енциклопедия. Искаме да говорим за средните линии на геометричните фигури и техните свойства.

В нашата работа е проследена верига от теореми, която обхваща целия курс на геометрията. Започва с теоремата за средната линия на триъгълника и води до интересни свойства на тетраедъра и други полиедри.

Средната линия на фигурите е отсечка, свързваща средните точки на двете страни на дадена фигура.

1. Свойства на централната линия

1. Свойства на триъгълник:

при начертаване и на трите средни линии се образуват 4 еднакви триъгълника, подобни на първоначалния с коефициент 1/2.
средната линия е успоредна на основата на триъгълника и равна на половината от него;
средната линия отсича триъгълник, който е подобен на дадения и неговата площ е равна на единицаедна четвърт от площта му.

2. Свойства на четириъгълник:

ако в изпъкнал четириъгълник средната линия образува равни ъгли с диагоналите на четириъгълника, тогава диагоналите са еднакви.
дължината на средната линия на четириъгълник е по-малка или равна на половината от сбора на другите две страни, ако тези страни са успоредни и само в този случай.
средите на страните на произволен четириъгълник са върховете на успоредника. Площта му е равна на половината от площта на четириъгълника, а центърът му лежи в точката на пресичане на средните линии. Този успоредник се нарича успоредник на Вариньон;
Пресечната точка на средните линии на четириъгълника е тяхната обща среда и разполовява отсечката, свързваща средите на диагоналите. В допълнение, това е центроидът на върховете на четириъгълника.

3. Свойства на трапец:

средната линия е успоредна на основите на трапеца и е равна на тяхната полусума;
средните точки на страните на равнобедрен трапец са върховете на ромба.

2. Триъгълник, четириъгълник, успоредник

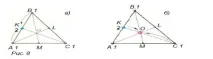
Към всеки триъгълник KLM могат да се прикрепят три триъгълника AKM, BLK, CLM, равни на него, всеки от които образува успоредник заедно с триъгълника KLM (фиг. 1). В същото време AK \u003d ML \u003d KB и три ъгъла граничат с върха K, равни на три различни ъгъла на триъгълника, общо 180 °, следователно K е средната точка на сегмента AB; по подобен начин L е средата на отсечка BC, а M е средата на отсечка CA.

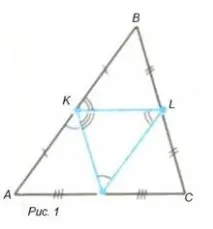
Теорема 1. Ако свържем средите на страните в произволен триъгълник, получаваме четири равни триъгълника, като средният е с всеки от другите три успоредника.

В тази формулировка всички три средни линии на триъгълника са включени наведнъж.

Теорема 2. Отсечка, която свързва средните точки на две страни на триъгълникуспоредна на третата страна на триъгълника и равна на половината от него (виж фиг. 1).

Свойството на средната линия на трапец следва от теоремата за средните линии на триъгълник (фиг. 2), както и от теоремата за сегментите, свързващи средите на страните на произволен четириъгълник.

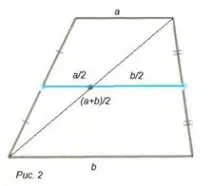
Теорема 3. Средите на страните на четириъгълника са върховете на успоредника. Страните на този успоредник са успоредни на диагоналите на четириъгълника, а дължините им са равни на половината от дължините на диагоналите.

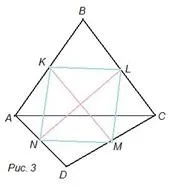
Действително, ако K и L са среди на страните AB и BC (фиг. 3), тогава KL е средната линия на триъгълника ABC, така че отсечката KL е успоредна на диагонала AC и равна на половината от него; ако M и N са среди на страните CD и AD, то отсечката MN също е успоредна на AC и равна на AC/2. Така отсечките KL и MN са успоредни и равни една на друга, което означава, че четириъгълникът KLMN е успоредник.

Като следствие от теорема 3 получаваме интересен факт (стр. 4).

Теорема 4. Във всеки четириъгълник сегментите, свързващи средните точки на противоположните страни, се разделят на две от пресечната точка.

В тези сегменти можете да видите диагоналите на успоредника (вижте фиг. 3), а в успоредника диагоналите са разделени от пресечната точка наполовина (тази точка е центърът на симетрия на успоредника).

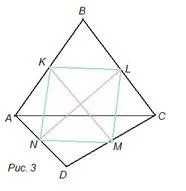
Виждаме, че теореми 3 и 4 и нашите разсъждения остават валидни както за неизпъкнал четириъгълник, така и за самопресичаща се четириъгълна затворена начупена линия (фиг. 4; в последния случай може да се окаже, че успоредникът KLMN е „изроден“ – точките K, L, M, N лежат на една и съща права линия).

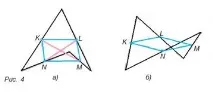
Нека покажем как от теореми 3 и 4 можем да изведем основната теорема за медианите на триъгълник.

Теорема5. Медианите на триъгълник се пресичат в една точка и го разделят в съотношение 2:1(броейки от върха, от който е изтеглена медианата).

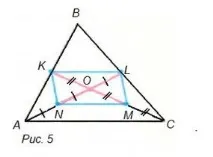
Нека начертаем две медиани AL и CK на триъгълник ABC. Нека O е точката на тяхното пресичане. Средите на страните на неизпъкналия четириъгълник ABCO са точките K, L, M и N (фиг. 5) - върховете на успоредника, а пресечната точка на неговите диагонали KM и LN за нашата конфигурация ще бъде пресечната точка на медианите O. Така че AN = NO = OL и CM = MO = OK, т.е. точка O разделя всяка от медианите AL и CK на съотношение 2:1.

Вместо медианата CK, можем да разгледаме медианата, изтеглена от върха B, и да се уверим по същия начин, че тя също разделя медианата AL в съотношение 2:1, т.е. минава през същата точка O.

3. Четириъгълник и тетраедър. Центрове на маса

Теореми 3 и 4 са верни и за всяка тримерна затворена начупена линия от четири връзки AB, BC, CD, DA, чиито четири върха A, B, C, D не лежат в една и съща равнина.

Такъв пространствен четириъгълник може да се получи, като изрежете от хартия четириъгълника ABCD и го огънете диагонално под определен ъгъл (фиг. 6, а). Ясно е, че средните линии KL и MN на триъгълниците ABC и ADC си остават както преди и ще бъдат успоредни на отсечката AC и равни на AC/2. (Тук използваме факта, че основното свойство на успоредните прави остава вярно за пространството: ако две прави KL и MN са успоредни на трета права AC, тогава KL и MN лежат в една и съща равнина и са успоредни една на друга.)

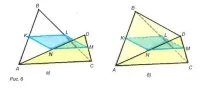
Така точките K, L, M, N са върховете на успоредника; по този начин сегментите KM и LN се пресичат и разделят пресечната точка наполовина. Вместо за четириъгълник, тук можем да говорим за тетраедър - триъгълна пирамида ABCD: средите K, L, M, N на нейните ръбове AB, AC, CD и DA винаги лежат в една и съща равнина. Разрязвайки тетраедъра по тази равнина (фиг. 6, b), получавамеуспоредник KLMN, две страни на който са успоредни на ръба AC и равни на

AC/2, а другите две са успоредни на ръба BD и равни на BD/2.

Същият успоредник - "средната част" на тетраедъра - може да бъде конструиран за други двойки противоположни ръбове. Всеки два от тези три успоредника имат общ диагонал. Средните точки на диагоналите са еднакви. Така получаваме интересно следствие:

Теорема 6. Три сегмента, свързващи средните точки на противоположните ръбове на тетраедъра, се пресичат в една точка и го разделят наполовина (фиг. 7).

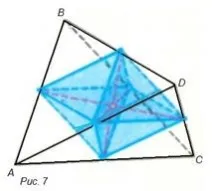
Този и други факти, обсъдени по-горе, естествено се обясняват на езика на механиката, с помощта на концепцията за центъра на масата. Теорема 5 говори за една от забележителните точки на триъгълник, точката на пресичане на медианите; в теорема 6, за забележителна точка за четирите върха на тетраедър. Тези точки са центровете на масата съответно на триъгълника и тетраедъра. Нека се върнем първо към теорема 5 за медианите.

Поставяме три еднакви тежести във върховете на триъгълника (фиг. 8).

Приемаме масата на всеки като единица. Намерете центъра на масата на тази система от тежести.

Нека първо разгледаме две тежести, разположени във върховете A и B: техният център на масата е разположен в средата на сегмента AB, така че тези тежести могат да бъдат заменени с една тежест с маса 2, поставена в средата K на сегмента AB (фиг. 8, а). Сега трябва да намерите центъра на масата на система от два товара: един с маса 1 в точка С, а вторият с маса 2 в точка К. Според правилото на лоста центърът на масата на такава система е в точка О, която разделя сегмента SC в съотношение 2: 1 (по-близо до товара в точка К с по-голяма маса - фиг. 8, b).

Бихме могли първо да комбинираме натоварванията в точки B и C, а след това - полученото натоварване с маса 2 в средата L на сегмент BC - с товара в точка A. Или първо да комбинираме натоварвания A и C, a. тогавадобави B. Така или иначе, трябва да получим същия резултат. По този начин центърът на масата се намира в точка O, разделяйки всяка от медианите в съотношение 2:1, като се брои от върха. Подобни съображения биха могли да обяснят и теорема 4 - фактът, че сегментите, свързващи средината на противоположните страни на четириъгълника, се разполовяват (те служат като диагонали на успоредника): достатъчно е да поставите еднакви тежести във върховете на четириъгълника и да ги комбинирате по двойки по два начина (фиг. 9).