Статистическа помощ

Най-простата корелационна система е линейна връзка между два признака - сдвоена линейна корелация.

Неговото практическо значение се състои в това, че има системи, в които сред всички фактори, влияещи върху продуктивния признак, се отделя един най-важен фактор, който основно определя изменението на ефективния признак. Измерването на двойни корелации е необходима стъпка в изследването на сложни, многофакторни връзки. Има такива системи от отношения, при изучаването на които трябва да се предпочита двойната корелация. Вниманието към линейните зависимости се дължи на ограничената вариация на променливите и факта, че в повечето случаи нелинейните форми на връзките се преобразуват в линейна форма за извършване на изчисления.

Двойното линейно корелационно уравнение се нарича двойно регресионно уравнение и има формата:

където y е средната стойност на резултантната характеристика > при определена стойност на знака на фактора x;

a - свободен член на уравнението;

b - коефициент на регресия, който измерва средното отношение на отклонението на резултантния признак от средната му стойност към отклонението на факторния признак от средната му стойност с една единица от измерването му - вариация y, за единица вариация x.

Що се отнася до термина регресия, неговият произход е следният: създателите на корелационния анализ Ф. Галтън (1822 - 1911) и К. Пиърсън (1857 - 1936) се интересува от връзката между растежа на бащите и техните синове. Ф . Галтън изследва повече от 200 семейства и открива, че в групата на семействата с високи бащи синовете са средно по-ниски от бащите си, а в групата на семействата с ниски бащи синовете са средно по-високи от бащите си. По този начин отклонението на растежа от средния вследващото поколение намалява – регресира. Причината е, че растежът на синовете се влияе не само от височината на бащите, но и от височината на майките и много други фактори в развитието на детето и тези фактори, произволно насочени както към увеличаване, така и към намаляване на височината, доближават растежа на синовете до средния ръст. Като цяло обаче вариацията във височината, разбира се, не намалява, а в нашето време на "ускорение" самата средна височина се увеличава от поколение на поколение.

Уравнение (8.4) се определя според данните за стойностите на признаците x и y в изследваната популация, състояща се от n единици. Параметрите на уравнението a и b се намират чрез метода на най-малките квадрати (LSM).

Първоначалното LSM условие за права линия има формата:

За да намерим стойностите на параметрите a h b, при които f(a, b) приема минималната стойност, ние приравняваме частичните производни на функцията на нула и трансформираме получените уравнения, които се наричат нормални уравнения на най-малките квадрати за правата линия:

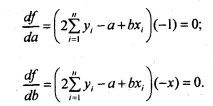
Следователно системата от нормални уравнения има формата:

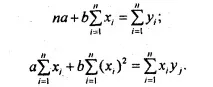
Нормалните уравнения на най-малките квадрати за права регресионна линия са система от две уравнения с две неизвестни a и b. Всички останали количества, включени в системата, се определят от първоначалната информация. Така при решаването на тази система от уравнения и двата параметъра на уравнението на линейната регресия се изчисляват еднозначно.

Ако първото нормално уравнение се раздели на n, получаваме:

Съгласно уравнение (8.6) на практика обикновено се изчислява свободният член на регресионното уравнение a. Параметърът b се изчислява по трансформираната формула , която може да бъде получена чрез решаване на системата от нормални уравнения за b:

. (8,7)

Тъй като знаменателят на този израз не е нищо повече от дисперсията на x, т.е. д. st 2 ^, тогава можем да напишем формулатакоефициент на регресия във формата:

(8-8)

Замествайки в (8.8) израза за σ 2 x , получаваме:

. (8,9)

Параметрите на регресионното уравнение могат да бъдат изчислени чрез детерминантите:

(8.10)

където Δ е детерминантата на системата;

Δ a е частична детерминанта, получена в резултат на заместване на коефициентите при a със свободни членове от дясната страна на системата от уравнения;

Δ b е частичен детерминант, получен чрез заместване на коефициентите при b със свободни членове от дясната страна на системата от уравнения.

Формулите (8.10) съответстват на най-общия подход за определяне на параметрите на уравнението на регресията и могат да се използват както в случай на двойна, така и в случай на множествена регресия.

Използването на една от формулите (8.7), (8.8) или (8.9) зависи от естеството на данните и наличието на показатели, вече изчислени на предишните етапи на анализа. Ако x беше изчислено? ,y? , σ x , σ y , тогава е по-лесно да се приложи формула (8.7) или (8.8). Ако изчисляването на параметрите на корелационното уравнение се извършва въз основа на първичните данни x i, y i, тогава формулата (8.9) е по-удобна. Особено значително намалява количеството на изчисленията със слаба вариация на знаците, тъй като тогава отклоненията на техните индивидуални стойности от средните стойности са с порядък или два по-малко от самите индивидуални и средни стойности. Освен това формула (8.9) изрично изразява стойността, посочена в n. 8.1 характеристика на корелационния анализ на връзките: корелационните параметри не зависят от нивата на характеристиките, а само от техните отклонения от средните стойности.

Ако стойността на атрибута се увеличи 10 пъти, корелацията няма да се промени и корелационните параметри няма да се променят, с изключение на свободния термин, ако се добави постоянно число към всички стойности на всеки атрибут.

Коефициентът на двойна линейна регресия, означен с b, имазначението на показателя за силата на връзката между вариацията на факторния признак x и вариацията на резултантния признак y. Той измерва средното отклонение на съвкупността от y от средната му стойност, когато знакът x се отклонява от средната си стойност с приетата мерна единица.

Например според табл. 8.1, когато цената на 1 крава се отклонява от средната с 1 rub. млечността на крава се отклонява от средната си стойност с 3,47 kg средно за населението. Ако факторът се отклонява с x? i-x? резултантният знак се отклонява средно с y? аз - у? .

Стегнатостта на сдвоената линейна корелация, както всеки друг индикатор, може да бъде измерена чрез съотношението на корелация η. В допълнение, с линейна форма на уравнението се използва друг показател за плътността на връзката - коефициентът на корелация r xy . Този показател е стандартизиран регресионен коефициент, т.е. д. коефициент, изразен не в абсолютни единици за измерване на знаци, а в дялове от стандартното отклонение на ефективния знак:

. (8.11

Коефициентът на корелация е предложен от английския статистик и философ Карл Пиърсън (1857 - 1936). Тълкуването му е следното: отклонението на признак-фактор от средната му стойност със стойността на средното му квадратично отклонение средно в популацията води до отклонение на признака-резултат от средната му стойност с r xy на средното му квадратично отклонение.

За разлика от коефициента на регресия b, коефициентът на корелация не зависи от приетите мерни единици на характеристиките и следователно е сравним за всякакви характеристики.

Обикновено една връзка се счита за силна, ако r ≥ . 0,7; средна плътност, при 0,5 ≤ r ≤ 0,7; слаб при r Не трябва, особено когато работите с компютър, да преследвате голямброя на знаците на коефициента на корелация. Първо, първоначалната информация рядко има повече от три значими точни цифри, и второ, оценката на близостта на връзката не изисква повече от две значими цифри.

Квадратът на коефициента на корелация се нарича коефициент на детерминация:

Тази формула ще е необходима за. множествен корелационен анализ. Умножавайки числителя и знаменателя (8.12) по получаваме:

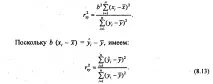
Този израз съответства на израза r \ 2 (виж формула (8.2)). Идентичността на коефициента на детерминация и квадрата на съотношението на корелация служи като основа за тълкуване на стойността на r 2 като дял от общата дисперсия на резултантния признак y, което се обяснява с изменението на признака - фактор x (и връзката между изменението на двата признака). Строго погледнато, коефициентът на детерминация (за линейната формула на връзката) или квадратът на съотношението на корелация трябва да се счита за основен показател за плътността на връзката. Но исторически коефициентът на корелация беше въведен по-рано, който дълго време се считаше за основен показател.

Подобно на различните "работещи" формули за изчисляване на регресионния коефициент, е възможно на базата на оригиналната формула (8.10) да се научат различни "работещи" формули за корелационния коефициент.

Разделяйки числителя и знаменателя на формула (8.11) на n, получаваме:

. (8.14)

Тази формула съответства на формула (8.8) за регресионния коефициент .

2. Стандартните отклонения могат да бъдат изразени по отношение на средните стойности на характеристиката:

Замествайки тези изрази в (8.14), получаваме:

. (8.15)

Тази формула (8.15) е по-удобна за изчисления, ако средните стойности на характеристиките и средните квадрати на отделните стойности са изчислени по-рано. Значението на коефициента на корелация се разкрива от оригиналаформула (8.11). В трансформираните формули това значение не е толкова ясно.

Нека разгледаме действителен пример за анализа на корелационната двойка линия на комуникация по данни на 16 селскостопански предприятия за разходите за 1 крава и добива на мляко от крава. Ограниченият обем на населението се приема само за образователни цели, за да се избегне носенето на обемисти маси (Таблица 8.1).

Средни стойности на характеристиките: x ? = 1605 рубли; в ? \u003d 35,2 c / глави.

Сравнявайки знаците за отклонения на знаците jc и y от средните стойности, виждаме ясно преобладаване на двойки отклонения, съвпадащи в знаци: има 14 от тях и само 2 двойки несъответстващи знаци.

Корелация между себестойността на крава и млечността