Тема 4 Множествена регресия

Фирмен номер, т.е

Печалба на i-тото предприятие, yi

Разходи за ново оборудване на i-то предприятие, хi1

Разходи за повишаване на квалификацията в i-то предприятие, хi2

Изградете двупосочна линейна регресия и оценете нейното значение. Нека въведем обозначението:

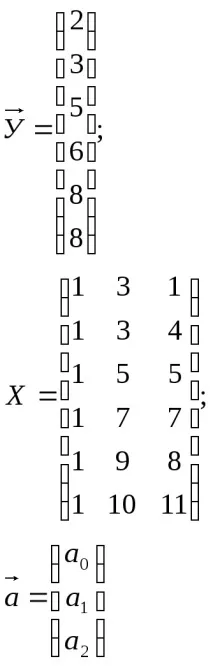
Транспонираме матрицата X:

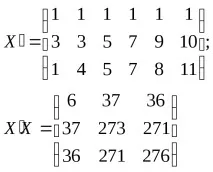
Инверсия на тази матрица:

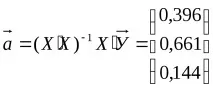
по този начин зависимостта на печалбата от разходите за ново оборудване и машини и от разходите за подобряване на уменията на служителите може да се опише чрез следната регресия:

Използвайки формула (5), където k=2, изчисляваме стандартната грешка на регресията S=0,636.

Изчисляваме стандартните грешки на регресионните коефициенти, използвайки формула (6):

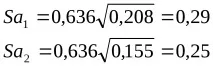
Нека проверим значимостта на регресионните коефициенти a1, a2. нека изчислим tcalc.

Избираме нивото на значимост

, броя на степените на свобода

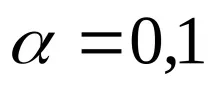
Нека оценим значимостта на коефициента a2:

Нека изчислим коефициента на детерминация по формулата (7)

. Печалбата на предприятието с 96% зависи от цената на ново оборудване и машини и повишаване на квалификацията с 4% от други и случайни фактори. Нека проверим значението на коефициента на детерминация. Нека изчислим Fcalc.:

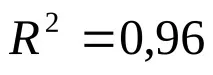
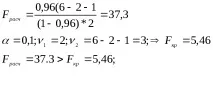
Че. коефициентът на детерминация е значим, регресионното уравнение е значимо.

От голямо значение при анализа, базиран на многомерна регресия, е сравнението на влиянието на факторите върху зависимия показател y. Регресионните коефициенти не се използват за тази цел поради разликите в мерните единици и различната степен на променливост. От тези недостатъци коефициентите на свободна еластичност са:

(11)

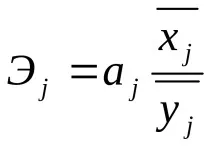
Еластичността показва колко процента се променя средно зависимият показател y, когато променливата

се промени с 1%, при условие че стойностите на останалите остават непромененипроменливи. Колкото по-голямо е, толкова по-голямо е влиянието на съответната променлива. Както при сдвоената регресия, за множествената регресия се прави разлика между точкова прогноза и интервална прогноза. Точкова прогноза (число) се получава чрез заместване на прогнозираните стойности на независимите променливи в уравнението на множествената регресия. Означава се с:

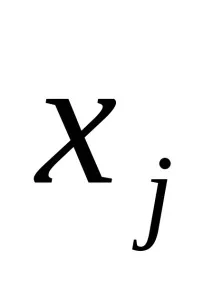
(12)

вектор на прогнозни стойности на независими променливи, след това точкова прогноза

(13)

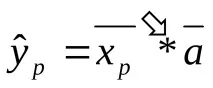
(14)

Стандартната грешка на прогнозиране в случай на множествена регресия се определя, както следва:

(15)

Избираме нивото на значимост α според таблицата за разпределение на Стюдънт. За нивото на значимост α и броя на степените на свобода ν = n-k-1 намираме tcr. Тогава истинската стойност на ur с вероятност 1- α попада в интервала:

(16)

Калкулатор

Услуга за безплатна оценка на цената на работата

1. Попълнете заявление. Експертите ще изчислят цената на вашата работа
2. Изчисляването на цената ще дойде по пощата и SMS

Номерът на вашето приложение

Точно сега по пощата ще бъде изпратено автоматично писмо за потвърждение с информация за приложението.

---