Температура на скалите и сондажната кал
Поведението на скалите върху стените на сондажа зависи от температурата на скалите и сондажната течност. Ето защо, за да се решат различни технически и технологични проблеми при пробиване на дълбоки кладенци, е необходимо да се знае температурата на скалите в дадена област и температурата на циркулиращата сондажна течност в различни участъци на сондажния канал. Това се обяснява с факта, че високата температура по време на процеса на сондиране може да окаже значително влияние: върху свойствата на сондажната течност и химикалите; върху условията на разрушаване на скалите; за работа на сондажни двигатели, битове, сондажни помпи и други елементи на циркулационната система на сондажната платформа.
Геостатичната температура на скалите T G (°C) е температурата в естествените условия на поява на скалите в земната кора, т.е. преди пробиване или след много дълъг престой на кладенеца без промиване.
С увеличаване на дълбочината на скалите под неутралния слой (скалния слой, който е най-близо до дневната повърхност, чиято температура не се променя с дневни и сезонни колебания в температурата на атмосферния въздух), той се увеличава и интензивността на растежа, като правило, се променя по-често в посока на намаляване.
В райони, където геотермалния градиент се променя много малко с дълбочината, разпределението на геостатичните температури може да се изчисли приблизително по формулата
T G ≈T pl -G(N pl -N), (1.37)
където T pl е известната температура на дълбочина Npl, °C; G - геотермален градиент - увеличение на T G за всеки megr от дълбочината на скалата, ° C / m (променя се до известна степен с дълбочината).
Потокът от сондажна течност (в сондажната колона) по време на движението си получава топлина от възходящия поток на сондажната течност (през стените на сондажната колона) и следователно постепенно се нагрява: в устието на кладенеца има минималентемпература и максимум на изхода от бита; ceteris paribus, тази температура се повишава с увеличаване на дълбочината на кладенеца.
По време на движението си възходящият поток на разтвора (в пръстеновидното пространство) отдава топлина на низходящия поток и започвайки от определена дълбочина, към стените на кладенеца; до тази дълбочина (при която температурата на калта е равна на температурата на стената на сондажа), възходящото течение получава топлина от стените на сондажа. По този начин циркулиращият разтвор се нагрява, когато се движи от дъното към определената дълбочина, и се охлажда, когато се движи от определената дълбочина към устието на кладенеца. Следователно температурата на сондажната течност трябва да се разглежда като най-важният параметър, който определя режима на сондиране и който може да бъде частично контролиран.
Изчисляването на разпределението на температурата на сондажната течност и стените на кладенеца по време на сондиране е доста сложно. Този въпрос е бил обект на множество разработки, използващи числени изчисления. Практическото им приложение обаче често е проблематично.
За приблизителна оценка на разпределението на температурата в кладенеца по време на промиване можете да използвате експресния метод на VNIIKR масло (1976).
Температура на дъното на кладенеца след няколко циркулационни цикъла
T 3 ≈0,33T 0 + 0,67T pl (1,38)
(T 0 - температура на неутралния слой на Земята, ° С); температура на потока в кладенеца
T out ≈0.67T 0 + 0.33T pl; (1,39)
температура на сондажната течност, изпомпана в сондажната колона (температура надолу по веригата на входа на сондажната колона)
T in = T out -∆T out (1.40)
(∆T out - намаляване на температурата на разтвора в системата за земна циркулация, в зависимост от температурата на атмосферата и дизайна на тази система и равно на 7 ° C);
средна температурасъответно възходящи и низходящи потоци по време на промиване
(1,41)
T sr.n ≈0.5 (T pl -T 0 +∆T out ); (1,42)
средна температура на кладенеца
T av.s ≈0,53T pl +0,45T 0 (1,43)
Температурата на циркулиращия сондажен флуид на всяка дълбочина h в кладенеца също може да се изчисли с помощта на формулата
Т h = T 0 + 0,14Гh + 0,43ГH. (1,44)
Въз основа на данните от извършените изчисления са построени криви на разпределение на температурата в низходящ и възходящ поток на сондажната течност.
Замръзналите скали, в зависимост от това колко дълго са в замръзнало състояние, се разделят на сезонно замръзнали (месеци) и вечно замръзнали (години, стотици и хиляди години). Дебелината на последните в северните и североизточните райони на България се измерва в стотици метри, а температурата достига – 7+ – 12°C
Кластичните наситени с вода рохкави и слабо циментирани скали по време на замръзване и размразяване драматично променят свойствата си: когато са замръзнали, те са циментирани с лед и се характеризират с висока якост (σ com ≤2,5 MPa) и непропускливост; когато се размразят, те преминават във водно състояние. Силата на замръзналите пясъчни скали е много по-висока от здравината на замръзналите глинести скали.
Пример 1.11 Оценете стойността на геостатичната температура, измерена на дълбочина H=1800 m, ако стойността на Tg, измерена на дълбочина 1500 m, е 64°C и средният геотермален градиент е 0,037°C/m.
Решение . По формула (1.37)
T g \u003d 64-0,037 (1500-1800) \u003d 75,1 ° C.
Пример 1.12 Постройте графика на разпределението на температурата в потока на сондажния флуид в края на сондажа на кладенец за следните условия: дълбочина на сондажа H=3200 m; геостатична температура T g =102°C; температура на неутралния слой на Земята T 0 =8°C; намаляване на температурата на сондажната промишленост на повърхносттациркулационна система ∆Т out ≈7°С.
Решение . Температурата на дъното на кладенеца по формулата (1.38) T 3 ≈0.33 8 + 0.67 102 \u003d 71 ° С.
Температурата на изходящия поток от кладенеца по формулата (1.39) Тout ≈0,67·8+0,33·102=39°С.
Температурата на сондажната течност, изпомпвана в сондажната колона, съгласно формулата (1.40)
Средната температура на възходящия и низходящия поток от изрази (1.41) и (1.42), съответно
T ср.v ≈4/9 8 + 5/9 102 = b0°C; T ср.n ≈0,5(102 - 8 + 7) = 50,5 °С.
Средната температура в кладенеца по формулата (1.43)
Tav.s ≈0,53 102+ 0,45 8 = 58°С.
Пример 1.13. Изчислете температурата на дъното на дупката за условията на предишния пример, ако геотермалния градиент Г=0,37°С.
Решение . По формула (1.44)
Th \u003d 8 + 0,14 0,037 3200 + 0,43 0,037 3200 \u003d 75,5 ° С.
Кривите на разпределение на температурата в низходящ и възходящ поток са показани на фиг. 1.2
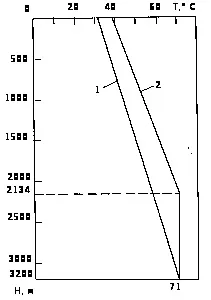
Ориз. 1.2. Криви на разпределение на температурата в низходящ (1) и възходящ (2) поток по време на промиване на сондажа за условията на пример 1.12.