Тип включване и изключване

Нека са дадени N обекта, от които N(a) - имат свойството a, N(a \ с черта над) -

Те нямат собственост а. N(a\)=N-N(a)

Нека има две свойства a1 и a2.

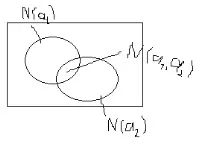
Брой обекти без свойства

половина в резултат на включване на всички N обекта, с изключение на броя на обектите, които имат едно свойство, включително обекти, които имат набор от 2 свойства, с изключение на обекти, които имат набор от 3 свойства.

N(a1\,a2\,am\)=N-N(a1)-…-N(an)+N(a1,a2)+N(an-1,an)-…+(-j)^n N(aj-a1)

Въпрос: Нека това е вярно за (n-1)-то свойство

13. Единични и множествени предикати.

P(x) - унарен пердикат

X - обект, предмет

х - Иванов, п - ученик

p(x, y) е двуместен предикат

обозначение на връзка - p, x, y - обекти

Инфиксна форма - в средата 2 > 3

Префикс - преди >(2,3)

Формите се занимават главно с бинарни отношения

Р(x,y,z) - триместно сказуемо

P(x) x принадлежи на M - обхвата на предиката (обекти, които могат да бъдат доставени на това място). За всяко x, принадлежащо на M, предикатът се превръща в твърдение, което приема всяка една стойност на истината

Пример: m P - четно число P \u003d

Всеки предикат дефинира някакъв набор от характеристики

P(x), (x принадлежи на M) P е набор от елементи, на които приема стойност true (т.е. състои се от онези елементи, на които P(x) е true)

P* - характеристична функция на множеството P

14. Логика на предикатите

В логиката на предикатите твърденията се разглеждат както структурно, така и смислово. Всяко изявлениезаявява, че даден обект има или няма някакво свойство, или че два обекта са в n области (?).

3) α-четна пропозиционална едноместна форма (превръща се в пропозиция след конкретизация)

Субектът е името на обекта, а името на свойството е името на предиката.

X брат Y е двуместна предложна форма.

Р(х) – едноместни предикати, х€М

P(x, y) - двуместни предикати, x, y € M (релация)

Фиксирането на α (стойността на обекта) произвежда твърдения, които понякога се наричат ​​единични твърдения.

P(x)*Q(x), където (*) е двоична операция (β,γ,→).

Ако е невъзможно да се установи логическа връзка между предикатите, тогава - двуместно.

Характеристичното множество p, дефинирано от предиката P(x), включва всички обекти, за които стойностите на предикатите са верни.

Характеристичната функция на набор може да приема стойности 0 или 1, а 1 - приема елементите на този набор.

---