Тълкуване на термини
Ролята на термините в езика на предикатната логика PrLе да описват имената на обекти от предметната областD. Самите термини обаче са само низове от знаци и не изразяват нищо, докато не се дефинира семантиката на езика, т.е. интерпретация на символи. За всеки n-местен функционален символ интерпретацията на IF преобразува множеството D n в D, т.е.
АКО:D n D. Очевидно можем да говорим само за тълкуване на постоянни термини. Наистина, ако е необходимо да се дефинира интерпретацията на lg (Sin(x)), веднага възниква въпросът какво е x. Следователно интерпретацията на формулите се състои от интерпретацията на всички термини, като се започне от тези, които имат най-голяма дълбочина на влагане.
Тълкуване на формула
Ако са дадени сигнатура , предметна област D и функция за интерпретация I, тогава казваме, че е даденаалгебрична система на сигнатураи я обозначаваме като подредена тройка (D,,I). Ако подписът не съдържа функционални символи, тогава алгебричната система на подписа се наричамодел. Интерпретацията на формулата в този модел е двойка (D, I), където I е преобразуване, във формата IR: D n , която свързва всеки подреден n-ke от обекти от D с логическа стойност 0-false или 1-true. В избраната интерпретация всяка затворена формула е един от начините за изразяване на стойността на истината на тази формула, а всяка отворена формула дефинира логическа функция на свободни променливи. Логическият смисъл на формулата A в интерпретацията на I се означава с I[A]. За постоянна формула това е 0 или 1, за формула, съдържаща свободни появявания на променливи, това е вектор, чиито елементи са 0 и 1, а дължината зависи от броя на различните набори от стойности на свободни променливи в дадена тематична област и от броя на постоянните атомарни подформули във формулата.
Интерпретацияатомни формули
Булевата стойност на постоянна формула може да бъде дефинирана като 0 или 1 (фалшиво или вярно) в този модел. В случай на параметрични формули, функцията за интерпретация определя стойността на формулата за всеки от възможните набори от променливи стойности в предметната област. Ако D е мощността на предметната област, n е местоположението на предикатния символ, тогава броят на различните набори от променливи стойности е равен на броя на разположенията с повторения на D елементи над n, т.е. D n = p. Тъй като във всеки набор от променливи стойности функцията за интерпретация може да приеме една от двете стойности (0 или 1), броят на различните интерпретации на предикатния символ е 2 p. Съответно интерпретацията се дава от двойката (D,Is), където Is е избраната функция за интерпретация
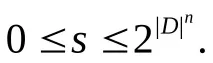
Пример 1.Нека предметната област е множеството от естествени числаN, а подписът съдържа единичен предикатен символ: "(x е просто число)".
Таблицата на интерпретационната функция е безкрайна, нейният фрагмент е даден в табл. 1.