топографска повърхност
Топографска повърхнина - раздел Обучение, Основни методи на проекция. Същността на проекционната операция Има голям клас повърхности, структурирани.
Има голям клас повърхности, чиято структура не подлежи на строго математическо описание. Такива повърхности се наричат топографски. Един от примерите за топографска повърхност е релефът на Земята.
Топографската повърхност се изобразява с помощта на контурни линии, получени чрез пресичане на земната повърхност с хоризонтални равнини, разположени на еднакво разстояние една от друга (фиг. 131).
По увеличаване или намаляване на контурните линии може да се прецени дали изображението е възвишение или низина.
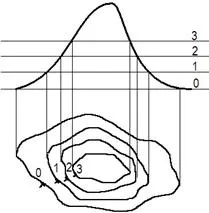
Профил на топографска повърхност – фигура, получена в резултат на разрез на повърхност с вертикална равнина.
За да се изгради профил на терена в дадена посока, топографска повърхност се пресича от вертикална равнина и пресечна линия на тази
равнини с топографска повърхност.
Задача.Построете линия на пресичане на равнина с топографска повърхност.
За да направите това, намираме пресечните точки на едноименните хоризонтали на равнината и повърхността (фиг. 132). Свързвайки точките с гладка линия („на ръка“), получаваме желаната пресечна линия.
Тази тема принадлежи към раздела:
Основни методи за проектиране. Същността на проекционната операция
Министерство на образованието и науката на България Казански държавен университет.
Какво ще правим с получения материал:
Всички теми в този раздел:
Казан 2010 Препоръчано за печат от Редакционно-издателския съвет на KSUAE Автор: Z.O. Галямова УДК74/744 LBC 30.11  
Приети означения и символи 1. Точки - с главни букви на латинската азбука: A, B, C, D ... или цифри 1, 2, 3, 4 ... 2. Прави и криви линии - с малки букви на латинската азбука: a, b, c, d .... 3. Повърхности
Централна проекция При метода на централната проекция всички прожектиращи лъчи преминават през обща точка S. Фигура 2 показва кривата ℓ с точки A, B, C и нейната централна проекция
Общи характеристики на проекция 1. Проекцията на точка е точка. 2. Проекцията на права линия - права линия (специален случай: проекцията на права линия - точка, ако правата линия минава през центъра на проекциите).
Ортогонални проекции (правоъгълни проекции или методът на Монж) Проекцията върху една проекционна равнина създава изображение, което не позволява недвусмислено определяне на формата и размерите на изобразения обект. Проекция на точка А (фиг.
Изграждане на допълнителна профилна равнина на проекции По-горе беше показано, че две проекции на точка определят нейното положение в пространството. Въпреки това, на практика, изображението на строителни конструкции, машини и различни инженерни
Октанти Проекционните равнини при взаимно пресичане разделят пространството на 8 тристенни ъгъла или октанти (от лат. Octans - осма част). Изчисляването им веде
Изображение на линия върху диаграма на Монж Най-простият геометричен образ е линия. В дескриптивната геометрия се приемат два метода за образуване на линия: 1. Кинематичен – разглежда се линията
Линия детерминанта Детерминантата е набор от условия, които дефинират геометрично изображение. Дефиниторът на линията е точка и насочена
Линии с частично положение Линиите с частично положение са прави линии, успоредни или перпендикулярни на която и да е проекционна равнина. Има 6пряка частна позиция,
Точка, принадлежаща на права Теорема: Една точка принадлежи на права, ако същите проекции на точката лежат върху същите проекции на правата (фиг. 21). &nbs
Следата на правата линия Хоризонталната линия М е пресечната точка на правата линия с хоризонталната проекционна равнина P1. Фронтална следа N - точка на пресичане на права линия с
Взаимно разположение на прави Две прави в пространството могат: да са успоредни, да се пресичат, да се пресичат. 1. Успоредни са две прави, които лежат
Определяне на видимостта на геометрични елементи Когато изобразявате непрозрачни обекти, за да направите чертежа по-ясен, е обичайно да рисувате проекции на видими елементи с плътни линии, а невидимите -
Теорема за прав ъгъл Теорема: Ако едната страна на прав ъгъл е успоредна на която и да е проекционна равнина, а другата страна не е перпендикулярна на нея, тогава това
Детерминанти на равнината Раздел 3 Равнината е най-простата повърхност от първи ред, дадена е от детерминантата: ∑ ( Г, А ), където: ∑ - обозначение p
Следи от равнина Следите от равнина се наричат пресечни линии
Обща позиционна равнина Обща позиционна равнина е равнина, която не е успоредна или перпендикулярна на никоя от проекционните равнини (фиг. 35). Всички рисунки
Равнини с частно положение В допълнение към разглеждания общ случай, равнината по отношение на равнините на проекциите може да заема следните частни позиции: 1.
Признак за принадлежност на точка и права на равнина Теорема 1: Една права принадлежи на равнина, ако минава през две точки, принадлежащи на тази равнина (фиг. 43). &n
Основните линии на равнината От всички прави линии, които могат да бъдат начертани в равнината, трябва да се подчертаеглавни линии, които включват: 1 Хоризонтална равнина
Преобразуване на чертеж Раздел 4 В дескриптивната геометрия задачите се решават графично. Броят и характерът на геометричните конструкции, докато,
Методът за замяна на проекционни равнини
Проекции Решаването на всички проблеми чрез замяна на проекционните равнини се свежда до решаването на 4 основни задачи: 1. Замяна на проекционната равнина, така че правата в общо положение да стане правата ur
Определяне на истинската дължина на сегмент от права линия по метода на правоъгълния триъгълник Както знаете, проекцията на права линия в общо положение има изкривена стойност. За определяне на естествената стойност на правата линия, в допълнение към горния метод, се използва
Методът на въртене около проектиращите оси При решаване на задачи за преобразуване на чертежа по метода на въртене, позицията на дадените геометрични елементи се променя чрез завъртането им около проектиращата ос.
Въртене около линията на нивото Този метод се използва за преобразуване на равнината на общото положение в равнината на нивото и за определяне на естествения размер на плоска фигура. Разрешавам проблем
Детерминант на повърхността Раздел 5 Повърхностите се разглеждат като непрекъснато движение на линия в пространството по определен закон, докато линия, която
Линейчати повърхности Линейчатите повърхности се образуват от непрекъснатото движение на права образуваща по определена направляваща, която може да бъде права линия, начупена линия или крива
Спирални повърхнини Спиралните повърхнини се образуват от спираловидно движение на права образуваща. Това е комбинация от две движения на генератора: транслационно движение
Повърхности на въртене (ротационни) Дефиниция на повърхнини на въртене Повърхностите на въртене се използват широко в архитектурата и строителството. Те най-ясно изразяват центричността на архитектурната композиция и освен това
Повърхнини, образувани от въртенето на равнинна крива Повърхнините от тази група се наричат повърхнини в общо положение. Алгоритъм за конструиране на повърхности (фиг. 70): 1.
Повърхности, образувани чрез въртене на права линия Детерминанта на повърхността: Σ ( i, ℓ ), където i е оста на въртене, ℓ е права линия.
Кръгове Квалификатор на повърхността: Σ ( i, ℓ ), където i е оста на въртене, ℓ е кръгът. а) сфера (топка)
Пресичане на повърхността на геометрично тяло с равнина Изграждането на линия на пресичане на повърхност с равнина се използва при формирането на форми на различни части на строителни конструкции, при чертане на сечения и планове
Взаимно пресичане на повърхностите на геометрични тела Архитектурни конструкции и сгради, различни фрагменти и детайли са комбинация от геометрични форми - призми, паралелепипеди, повърхности на въртене и по-сложни
Частни случаи на пресичане на повърхнини Има два случая на конкретно пресичане на повърхнини: 1. И двете пресичащи се повърхнини са издадени.
Общ случай на пресичане на повърхнини В този случай и двете пресичащи се повърхнини заемат общо положение в пространството спрямо проекционните равнини. Проблемите се решават с помощта на посредници, като
Изграждане на линия на пресичане на повърхности от втори ред по метода на концентричните сфери При пресичане на повърхности от втори ред, линията на пресичане в общия случай е пространствена крива от четвърти ред, която може да бъде разделена на две
Теорема на Монж Теорема: Ако две повърхности на въртене (от втори ред) са описани около или вписани в трета, тогава линията на пресичане на тяхното затихване
Пресичане на права линия с повърхност или равнина Задачите за определяне на точките на пресичане на права линия с повърхност (равнина) са основните позиционни задачи на дескриптивната геометрия, както и в конструкцията
Повърхностно разгъване Раздел 7 Разгъването е инженерен проблем, който се среща при изработката на технически части от тънък листов материал, като например вена обвивка
Разгъване на пирамида Проблем. Конструирайте развитие на пирамидата SABC. Определете позицията на точката М на метене (фиг. 98). Решение: Така че, за да изградите повърхностно разгъване, не го правете
Развиване на призма Фиг.98 При конструиране на разработка на странична повърхност на призма се използват 2 метода: 1. метод на нормално сечение; 2.
Разгъване на криви повърхности По принцип разгъването на криви повърхности се извършва по метода на триангулацията, т.е. чрез замяна на извита повърхност с вписана в нея фасетна повърхност
Развиване на прав кръгов конус Задача. Построете разработка на прав кръгов конус (фиг. 101). Решение: За да изградите размах, n-странно n
Развиване на скосен (елипсовиден) конус Задача. Построете разработка на кос конус. Поставете върху сканирането линията на пресичане на конуса с фронтално изпъкналата равнина ∑ (фиг. 102). Решение:
Разработване на прав кръгъл цилиндър Задача. Построете разработка на прав кръгов цилиндър (фиг. 103). Решение: Както в проблема, разгледан по-горе, n
Разгъване на сферични и торични повърхнини Сферичните и торични повърхнини са приблизително разгънати. Същността на конструкцията е в товасе изгражда размах на повърхността, като се разделя на равни части (фиг. 104) по меридианите и всяка
Същност на метода на проекциите с числови знаци
Изображение на права линия Правата линия може да бъде определена чрез проекции на произволни две нейни точки. И така, точка А се намира в пространството, нейната височина е 3 единици (фиг. 107).
Установяване, ексцес, интервал и наклон на правата На фиг. 109 показва правата линия AB и нейната проекция A1B3 върху нулев квадрат
Градуировка на права линия Градуировка на права линия - намиране на точки върху проекцията на права линия, които имат цели числа. Градуирането се основава на метода на пропорциите
Взаимно разположение на линии Позицията на две линии в пространството може да се определи от техните проекции върху равнината на нулевото ниво (P0), ако са изпълнени следните условия: 1. D
Изображение на равнината Равнината в проекции с цифрови маркировки се показва и определя от същите детерминанти, както в ортогоналните проекции, а именно:
Взаимно разположение на равнините Две равнини в пространството могат или да са успоредни една на друга, или да се пресичат под прав или остър-тъп ъгъл. 1.
Пресичащи се равнини (фиг.123): Пресичат се равнини, чиито мащаби на наклона не отговарят на поне едно от горните условия. Ориз. 122
Пресичане на права с равнина Задача. Построете пресечната точка на правата А4В7 с равнината, дадена от скалата на наклона ∑i. Решение:
Изображение на повърхности В разглеждания метод всички повърхности, независимо от метода на тяхното формиране, се изобразяват чрез проекции на техните хоризонталис белези, фиксирани
Повърхността на същия наклон (равен наклон) Повърхността на същия наклон е линейчата повърхност, всички праволинейни генератори на която са еднакви с определена равнина
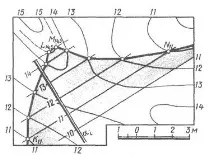
Изграждане на линията на най-големия наклон на топографската повърхност Линиите на наклона и същия наклон намират широко приложение в инженерната практика. Необходимо е да се знае посоката на линията на наклона, по-специално, за да се вземе необходимото
Определяне на границите на земните работи При проектирането на железопътни линии, магистрали, по време на строителството на строителни обекти е необходимо да се определи обемът на земните работи, извършени по време на строителството
Заключение Този учебник, както вече беше отбелязано, може да се използва от студенти от специалност 270106 "Производство на строителни материали, изделия и конструкции", 2
Ортогонални проекции (правоъгълни проекции или методът на Монж)…………………………. 9 1.5. Специални случаи на местоположение на точките в пространството ……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………торине 11 1.6. Изграждане на допълнителен профил
Пресечна точка на повърхнина на геометрично тяло с равнина……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………… ……………………………………………………………………………47 6.2. Взаимно пресичане на повърхнини на геометрични тела………………………………………….52 6.3. Свойства на изпъкналата повърхност………………..52 6.4
Дескриптивна геометрия (кратък курс) Учебно ръководство Редакционно-издателски отдел Подписано в p