Уравнение на Бернули
Днес решаваме задачи по теоремата на Ойлер за непрекъснатостта на струята и си припомняме уравнението на Бернули.
Уравнение за непрекъснатост на струята:
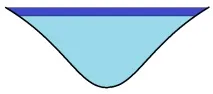
Речно корито в разрез

Речно корито. Разрез
Тук е скоростта на струята в сечението и е скоростта в сечението. Може да се заключи, че колкото по-тясна е тръбата, през която тече течността, толкова по-бързо тече. Ето защо течението на реката е по-бързо на повърхността, отколкото в дълбините и в средата на канала, отколкото близо до брега. Фигурата показва напречен разрез на речното корито, като зоните, където течението е по-бързо, са осветени в синьо.
Разбира се, разделянето на участъка на канала на зони е условно.
Тук е плътността на течността, е ускорението, дължащо се на гравитацията, и са височините на флуидния елемент над земята, и са скоростта на течността на тези височини, и са налягането на течността на тези височини. Уравнението може да се приложи както към течна, така и към газообразна среда.
Ако напишем уравнението по различен начин:
тогава отляво имаме разликата в налягането. Да предположим, че височината е една и съща, тогава уравнението ще бъде написано, както следва:
Тогава става ясно защо при силен вятър големите чаши могат да бъдат изстискани отвътре, защото вътре в стаята скоростта на вятъра е нула. Ако среда 1 е на открито, а среда 2 е на закрито, тогава налягането вътре в помещението е по-голямо от налягането отвън, така че екструзията ще настъпи навън.
Могат да се направят подобни разсъждения и може да се заключи, че покривите се откъсват по време на ураган по същата причина.
Задача1. Движението на въртящ се съд се основава на ефекта на Бернули. Вместо платна, този кораб има огромни вертикални цилиндри, които непрекъснато се въртят от двигатели. Да приемем, че духа постоянен южен вятър и кораб с този дизайн трябва да плава на изток. кактрябва ли да се въртят цилиндрите - по или обратно на часовниковата стрелка, ако ги гледаш отгоре?
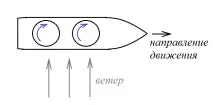
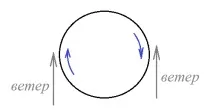
Разгледайте чертежа. Отляво вятърът, така да се каже, задвижва цилиндъра: скоростта на вятъра се добавя към скоростта на цилиндъра, а отдясно скоростта на вятъра е насочена срещу скоростта на цилиндъра, вятърът "забавя" въртенето му. Тогава, съгласно уравнението на Бернули, възниква положителна разлика в налягането: налягането пред цилиндъра по посока на движението е по-малко от налягането отзад. Тази разлика в налягането ще тласка кораба в посока отляво надясно, тоест на изток.
Отговор: по часовниковата стрелка.
Задача2. Водата тече през хоризонтална тръба с променливо напречно сечение. Скоростта на потока в хоризонталната част на тръбата е 20 cm/s. Определете скоростта на водния поток в тясната част на тръбата, чийто диаметър е 1,5 пъти по-малък от диаметъра на широката част.
Нека използваме уравнението за непрекъснатост на струята:
Нека е скоростта на водата в тясната част на тръбата и е сечението на тръбата в тясната част.
Нека изразим скоростта от него:
Напречното сечение на тръбата е кръг, площта на кръга в тясната част, в широката част.
Знаем за съотношението на диаметрите, което
След това можем да заместим числа в нашата формула (само не забравяйте да представите известната скорост в единици SI).
Отговор: скоростта на водата в тясната част е 0,45 m/s
Задача3. От лодка, движеща се със скорост km / h, тръба, огъната под прав ъгъл, се спуска във водата, така че спуснатият край на тръбата да е хоризонтален и да е обърнат към дупката по посока на движението. Другият край на тръбата, който е във въздуха, е вертикален. До каква височина спрямо нивото на водата в езерото ще се покачи водата в тръбата? Игнорирайте триенето.
Скоростта трябва да бъде изразена в единици SI: m/s
Скоростта на водата спрямо лодката също е 5 m/s. Това еводата има кинетична енергия. Когато водата се издига в тръбата, нейната кинетична енергия се преобразува в потенциална енергия: .
Тъй като няма триене, няма загуба на енергия, тоест можем да приравним:
Тогава височината на повдигане:
Задача4. В широка част на хоризонтална тръба маслото тече със скорост m/s. Определете скоростта на потока на маслото в тясната част на тръбата, ако разликата в налягането в широката и тясната част на тръбата е mm Hg. Изкуство.
Тук отново ще дойде на помощ уравнението на Бернули, от което можете да изключите термините, които включват височината на повдигане, тъй като по условие тръбата е разположена хоризонтално. Тогава уравнението ще приеме формата:
Преди да замените числата, е необходимо да изразите налягането в Pascals: