Урок по алгебра в 7. клас на тема Решаване на уравнения чрез техники за разлагане на полином
Секции: Математика
Момчетата, усвоили методите за факторизиране на полином за доста дълго време, стигнаха до момента, в който е необходимо да систематизират и обобщят изучаваните методи, да се опитат да направят нови открития и най-важното: да намерят интересно приложение на различни методи за факторизиране за решаване на уравнения, които понякога са идентични по смисъл.
1. Какво означава да факторизираме полином?
2. В кой случай произведението на множителите е равно на 0?
3. Степента на кое число е нула? 1??
4. Какви техники за факторизация знаете?(Поставяне в скоби на общия множител, групиране на членовете с последващо премахване на общия множител, използване на формули за съкратено умножение).
5. Колко е квадратът на сбора, разликата на два члена?
6. Каква е разликата между квадратите на два члена?
На дъската са написани уравнения:
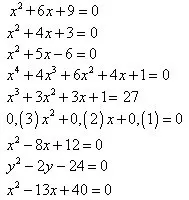
На какво основание тези уравнения могат да бъдат разделени на групи? (Уравнения, съдържащи полином от втора степен. Уравнения, съдържащи полином, по-голям от втора степен. Уравнение, съдържащо полином от втора степен, чиито коефициенти са периодични дроби).
Трябва да решим тези уравнения, като избираме различни решения, въпреки понякога сходството на уравненията.
Помолете учениците да решат уравнението по два начина. Извиквам двама ученика на дъската.
Единият ученик решава уравнението, като разделя монома 6x на сумата от два монома, а другият използва съкратената формула за умножение - квадрат на сумата:

Въпрос: Кой начин се оказа по-рационален?(Разбира се второто).Как може да се нарече?
(Избиране на пълния квадрат на сбора)
Обсъждаме решението на уравнението.
Възможно ли е да се реши уравнението, като се раздели един от членовете на две?
(Да,)
Какво ще кажете за подчертаване на пълния квадрат на сумата?
(трудно, тъй като 3 не е квадрат на нито едно рационално число)
И все пак, нека се опитаме да изолираме пълния квадрат на сумата: добавете сумата от първите два члена към квадрата на сумата.
Как можете да факторизирате полинома от лявата страна на уравнението?(По формулата за разликата на квадратите).
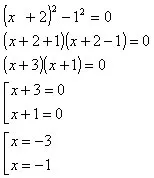
Помислете дали е възможно да се реши уравнението по подобен начин?
(Неудобно в този случай, числото 5).
И все пак нека се опитаме да следваме стриктно формулата за сумата на квадрата, когато избираме пълен квадрат:
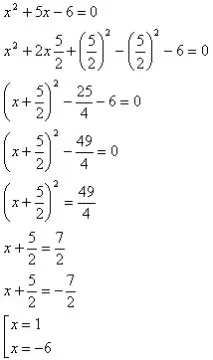
Обърнете внимание на коефициентите на уравнението. Какъв модел може да се види?
(прочетете същото отляво надясно)
Какво се случва с показателите на променливата x?
(намаляване с едно)
Дайте предположение за полинома от лявата страна на уравнението.
(Полиномът x 4 + 4x 3 + 6x 2 + 4x + 1 е (x + 1) 4). Обосновете го.
(Построете триъгълника на Паскал
14641 Четвъртият ред съдържа коефициентите на повишаване на бинома на 4-та степен (x+1)
И така, как ще изглежда уравнението? Решете го устно.
Решете уравнението устно
Какви числа са коефициентите на уравнението
(Периодични десетични знаци)
Преобразувайте периодичните дроби в обикновени дроби и решете полученото уравнение.
(Правилото за преобразуване на периодична десетична дроб в обикновена: за да преобразувате периодична десетична дроб в обикновена, трябва да извадите числото преди първата точка от числото преди първата точка и да направите товаразликата е числителя, а в знаменателя напишете числото 9 толкова пъти, колкото цифри има в точката и след деветката добавете толкова нули, колкото цифри има между запетаята и първата точка)
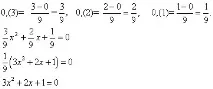
(Изберете рационално решение и намерете корените на уравнението, x=1 или)
Нека да разгледаме уравнението отново. Решаваме това уравнение по метода на неопределените коефициенти:
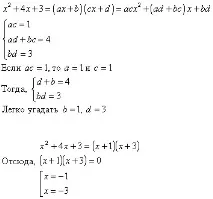
Сравнете стойностите на намерените корени със стойностите на променливитеbиd.(Те са противоположни)
Намерените корени потвърждават идеята, че независимо от метода на решение, корените не се променят.
Как уравнението е подобно на предишното?
(Коефициентът при x 2 е 1)
Нека се опитаме да решим това уравнение устно, без да използваме някой от разгледаните методи, но
като се вземат предвид някои разсъждения в предишния случай:
Запишете разширението на полином като произведение на биноми:
Тогава, кажете ми какво, стойностите на изразите ще бъдат ли равни и по аналогия с предишното разсъждение?
(Лесно е да се познае това или обратното).
Помислете на какво ще бъдат равни корените на уравнението?
Решете устно уравненията:
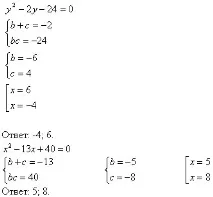
1. Какъв нов начин за решаване на квадратни уравнения срещнахте?
(Изолиране на пълния квадрат на сумата или разликата)
2. Защо мислите, че този метод не винаги е удобен?
(Например, в уравнението 3x 2 -2x-1=0 3x 2 не е квадрат на рационален израз)
3. Какво откритие направихте, като приложихте метода на неопределените коефициенти
решаване на квадратни уравнения, ако коефициентът на at е равен на 1?
(За да намерите корените, първо трябва да намерите две такива числа в и c, така че тяхната сума да е равна на втория коефициент, а произведението да е равно на третия член. И корените ще бъдат равничисла, противоположни на числата.
В 8. клас ще се запознаете с още един начин за решаване на квадратни уравнения – чрез формули. Разберете кой е Франсоа Виет и каква е връзката му с нашето откритие.