Урок в 9. клас - Система от уравнения, които се свеждат до квадрат

Секции: Математика

Цели на урока:

1. Повторете изучаваните по-рано различни методи за решаване на уравнения, които се свеждат до квадратни.
2. Да научи учениците на сътрудничество чрез работа в малки групи, както и на взаимопомощ в учебния процес. 3. Развитие на познавателен интерес, интерес към преподавателската дейност.

Форма на провеждане: Работа в малки групи, с участието на консултанти.

НАПРЕДЪК НА УРОКА

I. Организация на началото на урока.

Разделяне на групи

II. Съобщаване на студентите за целта на предстоящата работа. Учебна мотивация.

III. Интелектуална тренировка. (Приложение 1)

Загрявка под формата на тестови задачи. Подготовка за изпита.

IV. Проверка на самостоятелна домашна работа, насочена към повторение на основните понятия, основни знания, умения, методи на действие. Съветниците работят в борда. В предишния урок те получиха индивидуална домашна работа.

Системи от нелинейни уравнения, свеждащи се до квадратни. (приложение 2)

Решете система от уравнения

Решение: Ако извадим второто уравнение от първото, получаваме Значи трябва да решим системата от уравнения

където . Корените на това квадратно уравнение са . Ако y1=3, тогава от намираме x1=1. ако .

Отговор:

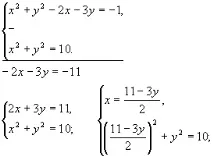
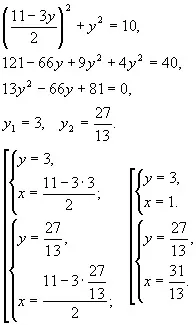
Отговор:

Метод за въвеждане на нови неизвестни при решаване на системи от уравнения. (приложение 3)

Решете система от уравнения

Решение. Означаваме с u и с v. Тогава системата ще приеме формата

Тоест получаваме система от две линейни уравнения с две неизвестни u и v. От първото уравнение, ние изразяваме u по отношение на v: и замествайки във второто уравнение, получаваме,откъдето v=2. Сега намираме u=1 и решаваме уравненията

Отговор:

Отговор:

Решете система от уравнения

Решение. Забележете, че условието е изпълнено за решенията на системата. Действително, от първото уравнение на системата следва, че ако , и числата не отговарят на второто уравнение на системата. Разделете първото уравнение на . Получете уравнението

Въвеждаме едно спомагателно неизвестно. Уравнението ще приеме формата. Това е квадратно уравнение с корени. Така от първото уравнение получаваме, че или или . Остава да заменим изразите и (като разгледаме и двата случая) във второто уравнение на системата. В първия случай получаваме уравнението , откъдето ; съответно . Във втория случай се получава уравнението, откъдето ; съответно

Отговор:

Възможен метод на проектиране

разделяме първото уравнение на , получаваме

Нека тогава

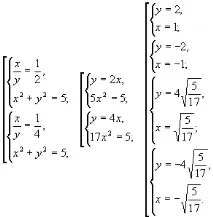
Отговор:

V. Работа в малки групи.

Решете система от уравнения

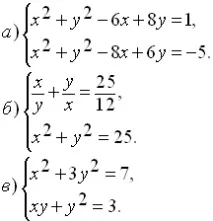
Решете система от уравнения

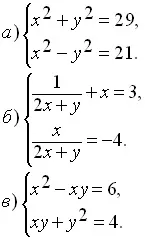
VI. Обобщаване на урока.

VII. Домашна работа.

Групова задача. Група консултанти изпълняват № 624 (4, 6, 8).

---