ВЕКТОРНА ДИАГРАМА графично представяне на стойностите на периодично променящи се количества и съотношения
ВЕКТОРНА ДИАГРАМА е графично представяне на стойностите на периодично променящите се количества и връзките между тях с помощта на насочени сегменти -вектори.
Векторните диаграми се използват широко в електротехниката, акустиката, оптиката и др.
Прости хармоники. функции на един период,
напр. може да се представи графично като проекция върху остаОy
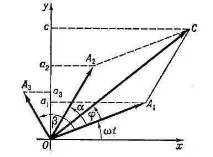
вектори, въртящи се с постоянна ъглова скорост и се завъртат спрямо ъглите . Дължината на векторите съответства на амплитудите на трептенията:
Сумата или разликата на две или повече трептения на векторната диаграма се обозначава като геометрична сума или разлика на векторите на компонентите на трептенията, получени съгласно правилото на паралелограма, а моментната стойност на желаната стойност се определя от проекцията на вектора на сумата върху оста
Например, изисква се да се намери сумата F от трептения с амплитуда , с амплитуда . С геометричното добавяне на вектори според векторната диаграма установяваме, че амплитудата на общото трептене F е равна на дължината на вектора и изпреварва по фаза трептението f с ъгъл
ВЕКТОРНО ИЗЧИСЛЕНИЕ, математическа дисциплина, която изучава свойствата на операциите върхувекториот евклидовото пространство. В този случай концепцията за вектор е мат. абстракция на величини, характеризиращи се не само с числова стойност, но и с посока (например сила, ускорение, скорост).
Произход и развитие на векторното смятане
Появата на векторното смятане е тясно свързана с нуждите на механиката и физиката. До 19 век само координатният метод беше използван за уточняване на вектори, а операциите върху вектори бяха сведени до операции върху техните координати.
Само в сер. 19 век с усилията на редица учени векторсмятане, при което операциите се извършват директно върху вектори, без да се прибягва до координатния метод на настройка. Основите на векторното смятане са положени от изследванията на английския математик У. Хамилтън и немския математик Г. Грасман върху хиперкомплексните числа (1844-50). Техните идеи са използвани от английския физик Дж. К. Максуел в работата му върху електричеството и магнетизма. Съвременната форма на векторното смятане е дадена от американския физик Дж. Гибс. Съществен принос за развитието на И. въведени от български учени. На първо място трябва да се отбележат произведенията на М. В. Остроградски. Той доказа основната теорема на векторния анализ (вижформулата на Остроградски). Изследванията на казанския математик А. П. Котелников върху развитието навинтовото смятанеса от голямо значение за механиката и геометрията. Тези изследвания бяха продължени от съветските математици Д. Н. Зейлигер и П. А. Широков. Голямо влияние върху развитието. И. имаше книга "Векторен анализ", написана през 1907 г. от българския математик П. О. Сомов.
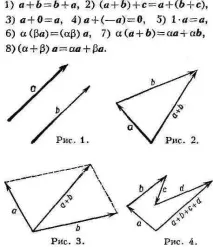
Векторна алгебра. Насочен сегмент се нарича вектор (фиг. 1), т.е. сегмент, за който са посочени началото (наричан още точката на приложение на вектора) и краят.
Дължината на насочен сегмент, представляващ вектор, се нарича дължина или модул на вектора. Дължината на вектораaсе означава с . За векторите се казва, че са колинеарни, ако лежат или на една права, или на успоредни прави. Два вектора се наричат равни, ако са колинеарни, имат еднаква дължина и еднаква посока. Всички нулеви вектори се считат за равни. Показано на фиг. 1 векторите a и b са колинеарни и равни.
Във векторното смятане се разглеждат свободни вектори.
Във векторната алгебра линейните операции върху вектори играят важна роля:операцията за добавяне на вектори и умножаване на вектор по реално число. Сумата отa + bвектори се нарича. вектор, преминаващ от началото на вектораaдо края на вектораb, при условие че началото на вектораbе прикрепено към края на вектораa(фиг. 2). Произходът на това правило се свързва с правилото на паралелограма за добавяне на вектори (фиг. 3), чийто източник е експерименталният факт за добавяне на сили (векторни величини) според това правило. Конструкцията на сумата от няколко вектора е ясна от фиг. 4. Произведението на вектораaс числото a се нарича. вектор, колинеарен на вектораa, имащ дължина, равна на и посока, съвпадаща с посоката наa, когато a>0.
Операциите за добавяне на вектори и умножаване на вектор по число имат следните свойства:
Във векторната алгебра често се използва концепцията за линейно зависими и линейно независими вектори.
Развитието и приложението на векторната алгебра е тясно свързано с различни видове векторни продукти: скаларни, векторни и смесени. Концепцията заскаларно произведениена вектори възниква, например, когато се разглежда работата на силаFпо даден път S: работата е равна на , където f е ъгълът между векторите F и S. Математически, скаларното произведение на векторите a и b се определя като число, обозначено с(а,b)и равно на произведението на дължините на тези вектори по косинуса на a въртя се между тях:
В диференциалната геометрия векторните функции на един аргумент се използват за дефиниране на криви. За определяне на повърхности се използват векторни функции на два аргумента.
Векторен анализ
В механиката, физиката и геометрията понятията за скаларни и векторни полета са широко използвани. Температурата на неравномерно нагрята плоча, плътността на нехомогенно тяло са физически. примери за съответно плоски ипространствено скаларно поле. Векторното поле образува множеството от всички вектори на скоростта на частиците на постоянен флуиден поток. Гравитационните, магнитните и електрическите полета също могат да служат като примери за векторни полета. напрежение на електромагнитното поле.
За математика. за задаване на скаларни и векторни полета се използват съответно скаларни и векторни функции. Ясно е, че плътността на тялото е скаларна функция на точка, а полето на скоростта на частиците на постоянен флуиден поток е векторна функция на точка. Мат. обикновено се нарича апарат за теория на полето. векторен анализ. За geom. характеристики на скаларно поле, използват се понятията за права и нивелирни повърхности. Линията на ниво на плоско скаларно поле се нарича. линията, на която функцията, която дефинира полето, има постоянна стойност. Нивелираната повърхност на пространственото поле се определя по подобен начин. Изотермите могат да служат като примери за линии на ниво - линии на ниво на скаларно температурно поле на неравномерно нагрята плоча.
За характеризиране на векторни полета се въвеждат редица понятия: векторна линия, векторна тръба, циркулация на векторно поле, дивергенция и вихър (ротор) на векторно поле.
Кочин Н. Е., Векторно смятане и началото на тензорното смятане, 6-то издание, L.-M., 1938;
Дубнов Я. С., Основи на векторното смятане, 4 изд., том 1-2, М., 1950-52;
Будак Б. М., Фомин С. В., Кратни интеграли и редове, 2 изд., М., 1967.