Вълни от материя
Как да тълкуваме факта, че в спектрите на елементите се появяват само определени характерни дължини на вълните?
Във физиката често се е случвало значителен успех да бъде постигнат чрез провеждане на последователна аналогия между очевидно несвързани явления. В тази книга често сме виждали как идеи, създадени и развити в един клон на науката, впоследствие успешно се прилагат в друг.
Развитието на механистичните възгледи и теорията на полето дава много примери от този вид. Сравняването на решени проблеми с нерешени проблеми може да даде нови прозрения и да хвърли нова светлина върху нашите трудности. Лесно е да се намери повърхностна аналогия, която всъщност не изразява нищо. Но да се разкрият някои общи съществени черти, скрити под повърхността на външни различия, да се създаде нова успешна теория на тази основа - това е важна творческа работа. Развитието на така наречената вълнова механика, започнало с работата на де Бройл и Шрьодингер преди около 15 години, е типичен пример за постиженията на една успешна теория, получена чрез дълбоки и успешни аналогии.
Нашата отправна точка е класически пример, който няма нищо общо със съвременната физика. Нека вземем края на много дълга гъвкава гумена тръба или пружина в ръцете си и я движим ритмично нагоре и надолу, така че краят да осцилира. Тогава, както видяхме от много други примери, вибрацията създава вълна, разпространяваща се през тръбата с определена скорост (фиг. 81). Ако си представим безкрайно дълга тръба, тогава групи от вълни, веднъж изпратени, ще последват безкрайното си пътуване без намеса.
Нека сега вземем друг пример. Двата края на една и съща тръба са фиксирани. Ако желаете, можете да използвате струна за цигулка. Какво се случва сега, че в единия край на гумената тръбаили струните създават вълна? Вълната, както и в предишния случай, ще започне своето пътуване, но скоро ще бъде отразена от другия край на тръбата. Сега имаме две вълни, едната, създадена от трептенето, а другата, създадена от отражението; те се движат в противоположни посоки и си пречат. Не би било трудно да се проследи интерференцията на двете вълни и да се определи природата на вълната, образувана от тяхното добавяне; нарича се стояща вълна. Тези две думи - "стоящ" и "вълна" - изглежда си противоречат, но комбинацията им е оправдана от резултата от наслагването на двете вълни.
Най-простият пример за стояща вълна е движението на струна с два фиксирани края нагоре и надолу, както е показано на фиг. 82. Това движение е резултат от факта, че една вълна се наслагва върху друга, когато и двете преминават в различни посоки. Характерна особеност на това движение е, че само две крайни точки остават в покой. Те се наричат възли. Вълната, така да се каже, се установява между два възела, всички точки на струната едновременно достигат максимума и минимума на своите отклонения.
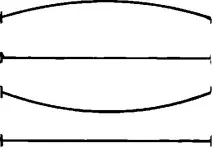
Но това е само най-простата форма на стоящи вълни. Има и други. Например една стояща вълна може да има три възела, по един във всеки край и един в средата. В този случай три точки винаги остават в покой. От фиг. 83 показва, че тук дължината на вълната е половината от дължината на вълната в примера с два възела. По същия начин стоящите вълни могат да имат четири (фиг. 84), пет възела или повече. Във всеки случай дължината на вълната ще зависи от броя на възлите.
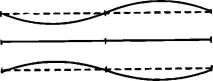
Това число може да бъде само цяло число и може да се променя само на скокове. Изречение като „Броят на възлите в стояща вълна е 3,576“ е чиста глупост. По този начин дължината на вълната може да се променя само прекъснато (дискретно).Тук, в този класически проблем, ние разпознаваме познатите характеристики на квантовата теория. Стоящата вълна, създадена от цигуларя, всъщност е още по-сложна, представляваща смес от много вълни с два, три, четири, пет възела или повече и следователно смес от различни дължини на вълната.
Физиката може да разложи такава смес на прости стоящи вълни, от които тя е съставена. Или, използвайки нашата стара терминология, можем да кажем, че вибриращата струна има свой собствен спектър, както и елемент, който излъчва радиация. И точно както в случая със спектъра на даден елемент, тук са разрешени само известни дължини на вълните, но други са забранени.
Така открихме известно сходство между вибрациите на струна и атом, излъчващ радиация. Странно е как може да съществува тази аналогия, но въпреки това ще направим още един извод от нея и ще се опитаме да продължим сравнението, тъй като го започнахме.
Атомът на всеки елемент се състои от елементарни частици: от тежки, които изграждат ядрото, и от леки - електрони. Такава система от частици се държи като малък акустичен инструмент, в който се създават стоящи вълни.
Стоящата вълна обаче е резултат от интерференцията на две или повече движещи се вълни. Ако има някаква истина в нашата аналогия, тогава една разпространяваща се вълна трябва да съответства на дори по-проста структура от структурата на атома. Коя е най-простата структура? В нашия материален свят нищо не може да бъде по-просто от електрон, елементарна частица, върху която не действат никакви сили, т.е. електрон в покой или в праволинейно и равномерно движение. Можем да добавим нова връзка във веригата на нашата аналогия: електрон, движещ се по права линия и равномерно? вълна с определена дължина. Това беше нова и смела идея на де Бройл.
По-рано беше показано, че има както явления, при които светлината проявява своя вълнов характер, така и явления, при които светлината проявява своя корпускуларен характер. Вече свикнали с идеята, че светлината е вълна, открихме, за наша изненада, че в някои случаи, например при фотоелектричния ефект, светлината се държи като поток от фотони. За електроните сега имаме точно обратната ситуация. Ние сме свикнали с идеята, че електроните са частици, елементарни кванти на електричеството и материята. Установени са техният заряд и маса. Но ако има някаква истина в идеята на де Бройл, тогава трябва да има явления, в които материята разкрива своя вълнов характер. Това заключение, поради факта, че следвахме акустичната аналогия, изглежда на пръв поглед странно и неразбираемо. Как може една движеща се частица да има нещо общо с вълна? Но такива трудности сме срещали във физиката повече от веднъж. Срещнахме същите проблеми в областта на светлинните явления.
Фундаменталните идеи играят съществена роля в създаването на физическа теория. Книгите по физика са пълни със сложни математически формули. Но началото на всяка физическа теория са мисли и идеи, а не формули. По-късно идеите трябва да приемат математическата форма на количествена теория, което прави възможно сравнението с експеримента. Това може да се обясни с примера на проблема, с който се занимаваме сега. Основното предположение е, че равномерно движещ се електрон ще се държи подобно на вълна при някои явления. Да предположим, че електрон или поток от електрони - ако приемем, че всички имат еднаква скорост - се движат равномерно. Масата, зарядът и скоростта на всеки отделен електрон са известни. Ако искаме по някакъв начин да свържем концепцията за вълна с равномерно движещ се електрон или електрони,тогава трябва да зададем следния въпрос: каква е дължината на вълната? Това е количествен въпрос и за да му се отговори, трябва да се изгради повече или по-малко количествена теория. Вярно, оказа се проста работа. Математическата простота на работата на де Бройл, която отговаря на този въпрос, е изключително изненадваща. По времето, когато работата му е написана, математическият апарат на други физически теории е бил относително усъвършенстван и сложен. Математическите операции в проблема материя-вълна са изключително прости и елементарни, но основните му идеи са дълбоки и далечни.
По-рано, в случай на светлинни вълни и фотони, беше показано, че всяко твърдение, формулирано на вълнов език, може да бъде преведено на езика на фотоните или светлинните корпускули. Същото важи и за електронните вълни. Корпускулярният език за равномерно движещи се електрони вече е известен. Но всяка позиция, изразена на корпускуларен език, може да бъде преведена на вълнов език, както беше в случая с фотоните. Две идеи доведоха до формулирането на правилата за превод. Една идея е аналогията между светлинните вълни и електронните вълни или между фотоните и електроните. Използваме един и същ метод на превод както за материята, така и за светлината. Друга идея идва от специалната теория на относителността. Законите на природата трябва да бъдат инвариантни спрямо трансформациите на Лоренц, а не класическите. И двете идеи водят до дефиницията на дължината на вълната, съответстваща на движещ се електрон. От теорията следва, че електрон, който се движи с, да речем, 16 000 km/s, има дължина на вълната, която може лесно да бъде изчислена и която се оказва, че лежи в същата област като дължината на вълната на рентгеновите лъчи. От това допълнително заключаваме, че ако е възможно да се открие вълновата природа на материята, тогава това може да бъде направеноекспериментално по същия начин, по който са открити вълновите свойства на рентгеновите лъчи.
Представете си сноп от електрони, който се движи равномерно с дадена скорост, или, ако използваме вълновата терминология, еднородна електронна вълна и предположим, че тя пада върху много тънък кристал, който играе ролята на дифракционна решетка.
Разстоянията между дифракционните елементи в кристала са толкова малки, че може да възникне рентгенова дифракция. Подобен ефект може да се очаква и за електронни вълни с дължина на вълната от същия порядък. Фотографската плака трябва да регистрира тази дифракция на електронни вълни, преминаващи през тънък слой кристал. Експериментът всъщност разкрива явлението дифракция на електронните вълни, което несъмнено е голямо постижение на теорията. Сходството между дифракцията на електронните вълни и дифракцията на рентгеновите лъчи е особено забележимо от сравнението на техните снимки (виж фиг. 80 и 85).

Ориз. 85. Дифракция на електронни вълни (Снимка от Лория и Клингер)
Знаем, че този модел ни позволява да определим дължината на вълната на рентгеновите лъчи. Това остава валидно и за електронните вълни. Дифракционната картина дава дължината на тези вълни, а пълното количествено съответствие между теорията и експеримента брилянтно потвърждава правилността на нашите разсъждения.
Тези резултати разшириха и задълбочиха предишните ни трудности. Това може да се изясни с пример, аналогичен на този, използван за светлинна вълна. Електронен снаряд с много малка апертура ще се отклони като светлинна вълна. Светли и тъмни пръстени се намират върху фотографската плака. Има известна надежда да се обяснят тези явления чрез взаимодействието между електрона и ръба на дупката, въпреки че такова обяснение не изглежда многообещаващ. Но какво се случва в случай на две дупки? Вместо пръстени се появяват ивици. Защо наличието на втората дупка обръща ефекта? Електронът е неделим и може, изглежда, да премине само през една от двете дупки. Как би могъл електрон, преминаващ през дупка, да разбере, че на известно разстояние има друга дупка?
Питахме се: какво е светлина? Дали е поток от корпускули или вълни? Сега питаме: какво е вещество, какво е електрон? Дали е частица или вълна? Електронът се държи като частица, когато се движи във външно електрическо или магнитно поле. Той се държи като вълна, когато се дифрактира през кристал. С елементарния квант на материята преминахме през същите трудности, които срещнахме при изучаването на светлинните кванти.
Един от най-фундаменталните въпроси, поставени от съвременния напредък в науката, е въпросът как да се примирят две противоречиви гледни точки за материя и вълна. Това е една от онези фундаментални трудности, които, веднъж формулирани, трябва да доведат, макар и по дълъг път, до прогреса на науката. Физиката се е опитала да разреши този проблем. Бъдещето ще покаже дали предложеното от съвременната физика решение е окончателно или временно.