Въртяща се черна дупка
Според теорията на Нютон гравитационното поле във всеки момент се определя изцяло от моментното разпределение на масите. По този начин гравитационното поле на неподвижна топка и въртяща се топка е абсолютно еднакво, само ако масите им са еднакви. Според теорията на Айнщайн това не е така и гравитационните полета на разглежданите топки ще се различават донякъде. В какво. това разлика ли е?
Тази разлика може да си представим най-ясно (но донякъде опростено), сякаш около въртящо се тяло възниква допълнително вихрово гравитационно поле, което увлича всички тела в кръгово движение около източника на полето. Материята се случва по такъв начин, сякаш слоевете на пространството бавно се въртят около такова тяло, а ъгловата скорост на тяхното въртене зависи от разстоянието: тя е малка далеч и се увеличава с приближаването към тялото. За обикновените небесни тела тези ефекти са незначителни. Най-лесният начин да ги откриете е да поставите жироскоп близо до въртящото се тяло. Ако тялото не се върти, тогава жироскопът ще показва постоянна посока в пространството по отношение на далечните звезди.
Използването на жироскопи е широко известно, например, за ориентиране на космически кораби. Въпреки това, близо до въртящо се тяло, жироскопът бавно се върти по отношение на далечни звезди. И така, близо до повърхността на въртящата се Земя, жироскопът се върти с около 0,1″ на година. Разбира се, такава незначителна скорост на въртене на жироскопа не може да попречи на ориентацията на космическия кораб. Освен това този ефект все още не е наблюдаван експериментално.
На повърхността на неутронни звезди (пулсари) ъгловата скорост на въртене на жироскопа може да бъде много голяма, само няколко пъти по-малка от скоростта на въртене на самата неутронна звезда. А самите неутронни звезди могат да се въртят със скорост от няколко десетки или повече оборота надай ми секунда. По този начин, жироскоп близо до такава бързо въртяща се звезда може да направи много обороти в секунда!
Какво ще се случи при релативистичния колапс на звезда с тази вихрова компонента на полето? Оказва се, че няма да се промени, както не се променя и сферичното гравитационно поле. Този вихров компонент на гравитационното поле се определя изцяло от общия ъглов импулс на тялото, от което произлиза черната дупка. По този начин ъгловият момент е третият числов параметър, който характеризира черна дупка.
Вихровият компонент на гравитационното поле нараства близо до черната дупка и действието му близо до самата граница на черната дупка води до важни последствия. Но първо, нека намерим повърхност, върху която гравитационната сила, действаща върху неподвижно тяло, се обръща към безкрайност. Спомнете си, че при липса на въртене такава повърхност е сферата на Шварцшилд. С други думи, това е границата на черна дупка (или, както се казва, хоризонта), от която нищо не може да излезе. При наличие на ротация това не е така. Гравитацията достига до безкрайност извън хоризонта, на повърхността, наречена границата на ергосферата. На тази повърхност и под нея никаква сила не може да задържи тялото в покой. Всяко тяло ще бъде отнесено от вихровия компонент на гравитацията в движение спрямо черната дупка. Но за разлика от телата под сферата на Шварцшилд (при липса на въртене), където те падаха неудържимо към центъра, тук, под границата на ергосферата, всички тела са въвлечени във въртеливо движение около черната дупка. В този случай тялото изобщо не е длъжно да се движи към центъра. Тя може както да се приближи, така и да се отдалечи от черната дупка, може да премине границата на ергосферата, като се движи както навътре, така и навън. Въпросът е как гравитационната сила действа върху тялото подграницата на ергосферата, ако безкрайна гравитационна сила действа върху нея вече на границата?
Тук трябва да си припомним какво вече казахме, когато обсъждахме гравитационната сила, действаща върху повърхността на Шварцшилд.
Гравитационната сила е безкрайна на границата само за неподвижно тяло, а ако тялото се движи с ускорена скорост, тогава силата ще бъде различна. При кръгово движение около черната дупка в същата посока като посоката на въртене на черната дупка, силата както на границата на ергосферата, така и вътре в нея се оказва крайна. Следователно тялото може да се движи в кръг вътре в границата на ергосферата, без да пада в центъра. По този начин, при наличие на въртене, статичната граница (т.е. границата на областта, където тялото може да бъде в покой спрямо черната дупка) се различава рязко от сферата на Шварцшилд при липса на въртене.
Виждаме, че границата на ергосферата изобщо не е границата на черна дупка, тъй като човек може да излезе навън изпод тази повърхност. Нека да видим какво ще се случи, когато се приближим до черната дупка.
Движейки се по-дълбоко, най-накрая достигаме до границата на черната дупка - хоризонта. На тази повърхност и под нея тялото (и всички частици и светлина) се движат само във вътрешността на черната дупка. Тук движението навън е невъзможно и никаква информация не може да достигне до външен наблюдател изпод този хоризонт.
Това е пространството между хоризонта и границата на статиката, което се нарича ергосфера. Там силата на гравитацията кара всички тела да кръжат около черната дупка (структурата на въртяща се черна дупка е показана на фиг. 6).
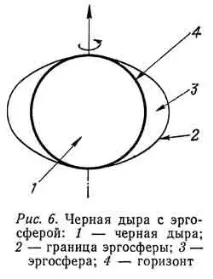
Черна дупка с ергосфера
Ако бавно приближите жироскопа към повърхността на ергосферата, неговата ъглова скорост на въртене ще нараства през цялото време, клонейки към безкрайност на самата повърхност (за неподвижен жироскоп).
Как да външнонаблюдател, ще се случат събития, когато тяло падне от голямо разстояние във въртяща се черна дупка?
Тяло, попадащо в черна дупка, първо ще се отклони в движението си по посока на въртенето си, ще пресече границата на ергосферата и постепенно ще се приближи до хоризонта. На хоризонта всички тела имат една и съща ъглова скорост на циркулация, независимо къде падащото тяло се удари на повърхността на хоризонта. Това е много важно свойство на въртяща се черна дупка. В самата ергосфера ъгловите скорости на телата могат да бъдатразлични,но когато се ударят в повърхността на черна дупка, телата вече иматедна и същаъглова скорост. Те се въртят заедно с повърхността на черната дупка, сякаш са залепени за повърхността на въртящо се твърдо тяло.
За външен наблюдател получената от тях светлина бързо става все по-червена и по-малко интензивна, след това напълно избледнява и те стават невидими за външен наблюдател: това, което се случва под хоризонта, той не вижда. Ако наблюдателят падне свободно във въртяща се черна дупка, то за крайно време той ще достигне хоризонта, както при невъртяща се дупка, и ще продължи да пада навътре. Нека засега оставим този наблюдател и се върнем в открития космос, в околностите на черната дупка.
Ъгловата скорост, обща за всички падащи тела върху хоризонта на черна дупка, е скоростта на нейното въртене. Определя се от израза Omega = 4pl/MS, къдетоlе ъгловият момент на тялото, от което произлиза черната дупка,Mе масата на черната дупка, S е площта на нейния хоризонт.
Обърнете внимание, че ъгловият импулс на черна дупка с дадена масаMне може да бъде произволно голям. Факт е, че когато тяло, което се върти достатъчно бързо, се компресира, на екватора възникват центробежни сили, които предотвратяват компресирането му вравнини на екватора. Тялото може да продължи да се свива само по полюсите. Но тогава ще се превърне в "палачинка" с радиус, много по-голям от гравитационния радиус, и няма да се появи черна дупка. Максимално възможният ъглов импулс на черна дупка и нейната максимална ъглова скорост на въртене се определят от факта, че по време на образуването на черна дупка линейната скорост на въртене на точките на екватора не надвишава скоростта на светлината. По ред на величината максималната ъглова скорост е равна на отношението на скоростта на светлината към гравитационния радиус: Omegamax=c/rg. За черна дупка с маса, равна на масата на Слънцето, тази ъглова скорост е равна на Qmax
Очевидно е, че черна дупка със скорост на въртене, по-голяма от максималната, не може да се появи, но възниква въпросът дали е възможно да се увеличи скоростта на въртене на черна дупка, след като се е появила, като я „завърти“ чрез хвърляне на частици в черната дупка (по определен начин), които носят със себе си ъглов момент.
Най-общо казано, по този начин е възможно да се увеличи ъгловата скорост на въртене, но масата на черната дупка също се променя. И ето какво се оказа: след като въртенето на черната дупка достигне своя максимум, тя е в състояние да улови само частици, които могат да променят нейното въртене и маса по координиран начин, така че въртенето да не стане по-голямо от максимума за дадена маса. Хвърляйки в черна дупка частици с ъглов момент, противоположен на ъгловия момент на черната дупка, ние ще намалим нейното въртене. Ако уловената частица не се е движила в равнината на екватора на черната дупка, тогава положението на полюсите на черната дупка, т.е. ориентацията на нейната ос на въртене, също ще се промени.
Гравитационното улавяне на частици от въртяща се черна дупка е малко по-различно от гравитационното улавяне от невъртяща се черна дупка. Частиците ще бъдат най-лесно уловени от него,които в близост до черната дупка летят в посока, обратна на въртенето, и с много по-голяма трудност летящите частици имитират черната дупка в посоката на въртене. Може да се представи визуално така, сякаш вихровият компонент на гравитационното поле около черната дупка би действал като прашка - ускорявайки и по този начин изхвърляйки частиците, движещи се покрай черната дупка в същата посока като завихрящия се "вихър" на това поле, и, обратно, забавяйки и улавяйки частиците, движещи се срещу "вихъра".
Помислете например за улавянето от максимално бързо въртяща се черна дупка на лъч светлина, движещ се в равнината на екватора на черната дупка. Спомнете си, че в случай на невъртяща се черна дупка, за да бъде уловен, светлинният фотон трябва да се приближи до черната дупка на разстояние 1,5rg. Далеч от черната дупка светлинният лъч се характеризира с ударния параметърlcap = 3Root3rg/2.
В случая на въртяща се черна дупка, разглеждана тук, лъчът в посоката на въртене трябва да има много по-малък параметър на въздействие:lcapture, 1 =rg\2,Но за лъч, идващ от противоположната страна, критичният параметър на въздействие е много по-голям:lcapture,2 = 4rg.
Ситуацията се променя и с кръговите орбити. За черна дупка без ротация последната стабилна кръгова орбита има радиус 3rg, частицата, движеща се по нея, има скорост 0,5s.И най-важното: за да влезе в тази орбита, частица с масаmтрябва да отдели енергия DeltaE = 6%mc 2(например под формата на гравитационно излъчване).
В случая на най-бързо въртящата се черна дупка, последната кръгова орбита се намира много по-близо до хоризонта, дълбоко в ергосферата. Но тук частицата може да се движи само в посоката на въртене на черната дупка. Енергията, коятоизлъчва частица, която е попаднала в тази орбита, много повече, отколкото за невъртяща се черна дупка, и е DeltaE = 42%mc 2 ,В същото време последната стабилна орбита на частица, въртяща се около черната дупка в обратна посока, се намира извън ергосферата и частица, падаща върху нея, освобождава само DeltaE = 4%mc 2енергия.