Въведение_v_kompyuternuyu_grafiku - Страница 6

Моливи от прави линии, успоредни на OX ( 1 0 0 0 ) и OY ( 0 1 0 0 ), преходни

dyat в сноп от прави линии с центрове

Ако има две точки на изчезване, тогава кубът ще изглежда така (фиг. 7):

Ориз. 7. Изображение на куб с две главни изчезващи точки по осите OX и OZ

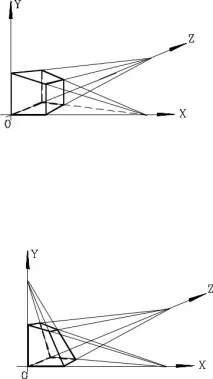
Изображението на куб в присъствието на три точки на изчезване (основните, разположени на осите) изглежда така (фиг. 8).

Ориз. 8. Изображение на куб с три основни точки на изчезване

3.4. Геометрични сплайни

Терминът идва от английското spline - така наречената гъвкава лента от стомана, с която се изчертават плавни криви през дадени точки. Този метод за конструиране на криви се използва при конструирането на лодки и корабни корпуси с гладки контури. Ако си припомним, че Англия исторически се развива като велика морска сила, тогава произходът на термина от английския термин за корабостроене е съвсем разбираем.

На първия етап това беше решение на проблема с апроксимацията на функциите в теоретично и практическо отношение. Тогава се установи, че самите сплайнове са много разнообразни и приложими в различни области: числени методи, системи за компютърно проектиране, автоматизация на научни изследвания, CG и др.

компютри, използващи сплайн теорията

приближения, стана възможно да се опише достатъчно

повърхности по прости формули.

Ако се опитаме да опишем цялото достатъчно голямо

отгоре като цяло, тогава

простите формули не са достатъчни. Приложение

същите прости формули са предпочитани в много случаи.

Следователно на практика се взема малка площ от повърхността и

голям брой така наречени референтни точки върху него и чрез тези точки аповърхност. За такива повърхности е необходимо и тяхното аналитично представяне с помощта на сплайни.

Визуализацията на такива криви и повърхности веднага позволява да се оцени какво се получава в резултат на дизайна и, ако е необходимо, да се направят промени в описанието на повърхностите.

Сама по себе си, теорията на сплайновете в момента е доста широка; по-долу ще разгледаме само проблемите на геометричното моделиране при проектирането на криви и повърхности.

Типична задача: да се построи крива от набор от точки в равнина или пространство

− преминаване през тези точки (интерполация);

− преминаване близо до тези точки (изглаждане).

Като пример на фиг. 13 е показана горната крива - интерполираща, долната - изглаждаща.

Два проблема едновременно:

− в кой клас криви да се търси желаната;

Нека да разгледаме първия проблем.

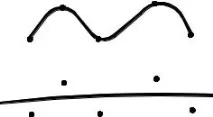
Фиг.13. Примери за интерполиращи (горни) и изглаждащи (долни) криви за един и същи набор от точки

Едно от изискванията е уникалността на решението на проблема. Второ, построената крива трябва да се променя плавно.

Нека на равнината е дадено множество от точки (x, y), i = 0, 1. м, и

и ще търсим крива в класа на многочлените (полиномите).

3.4.1. Интерполационен полином на Лагранж

Известен е полином, носещ името на Лагранж

( x 0 − x 1 ) * ( x 0

( x − x 0 ) * ( x − x 2 ) *. *( х

( x 1 - x 0 ) * ( x 1 - x 2 ) *. * ( x 1 − x n )

( x − x 0 ) * ( x − x 1 ) *. * ( x − x n − 1 )

( x n − x 0 ) * ( x n − x 1 ) *. * ( x n − x n − 1 )

Фактът, че тази функция е полином, може да се види от нейната форма. Всички стойности на x и y с индекси са просто числа, а функционалната зависимост се дава от произведението на поредица от фактори, където навсякъдепоявява се израз като (x - x 0) и т.н. Лесно се вижда, че по конструкция този полином е такъв, че описаната от него крива минава през всички дадени точки. Всъщност, ако вземем x \u003d x 0, тогава първата дроб (факторът пред y 0) се превръща в единица, а останалите - в 0. В резултат на това с тази стойност x \u003d x 0 получаваме y (x 0) \u003d y 0. По същия начин, за x \u003d x 1, се оказва

y (x 1) \u003d y 1 и т.н.

Ако трябва да изградите интерполационен полином на Лагранж само за две точки (x 0, y 0), (x 1, y 1) и такава задача също може да бъде поставена, тогава нейният израз ще бъде

и това е уравнението на права линия, минаваща през дадените точки. За дадени три точки получавате обикновена парабола, за четири точки - куб

парабола и др. Ако броят на дадените точки, номерирани от 0 до m, е m + 1, то степента на съответния полином на Лагранж е с една по-малка и равна на m.

1) полиномът се конструира просто и съответният израз, ако е необходимо, лесно се програмира;

2) полиномът е еднозначно определен, т.е. за даден набор от стойности

стойности x i и y i неговият израз винаги се оказва един и същ;

3) както за всеки полином, така и за полинома на Лагранж има производна от всякакъв ред (няма значение, че от реда на производната, по-висок от степента на полинома, тези производни изчезват - те все още съществуват).

1) с увеличаване на броя на точките, степента на полинома ( m в m точки) също се увеличава и степента на отклонение на кривата от апроксимираната зависимост се увеличава;

2) промяната или добавянето на поне една точка води до промяна на целия полином.

Но най-неприятният е следният недостатък на полинома на Лагранж. Ако построите крива, минаваща през всички дадени точки, тогава тя ще се окаже с голям бройточки на силно осцилиращи, т.е. силно се отклонява от средната стойност между две съседни точки. И въпреки че в този случай кривата все още минава през всички дадени точки, производните (които съществуват до произволен ред) могат да имат всякакви стойности между две точки, а не тези, които съответстват на общия характер на зависимостта

y = y(x). В това отношение кривите на фиг. 13 са характерни: горната интерполираща крива минава през всички дадени точки, както трябва да бъде в съответствие с дефиницията. Въпреки това, ако вземем производната - и нейната стойност се определя като тангенс на наклона на допирателната към кривата - тогава през целия интервал наклонът на съответната допирателна се променя много забележимо от точка до точка. Ясно е, че "средната" стойност на производната ще бъде много по-добра, ако се определи от изглаждаща крива.

Вторият, по отношение на противоположния, метод на приближение е с помощта на прекъсната линия. В този случай в някои области ще има

идеална линейна апроксимация, но в ъгловите точки, съвпадащи с точките x i, първите производни претърпяват прекъсване, т.е. имат различни стойности отдясно и отляво на точката.

Компромисът се постига чрез апроксимиране на кривата (полином) в отделни участъци - не цялата крива наведнъж, а последователно, участък по участък. След това се извършва гладко конюгиране на отделни секции чрез подходящ избор на коефициенти на полином. Това е централната идея

3.4.2. Кубични сплайни

Резултатът от такова приближение се нарича или просто сплайн. Аналогията с рисуването на сплайни е съвсем очевидна. Освен това, ако вземете гъвкава стоманена линийка и я използвате, за да начертаете крива през поредица от опори, се оказва, че кривата ще бъде

е графика на функцията y (x) във всеки участък между опорите - полиномтрета степен. На целия интервал x 0 , x 1 , . , x m този полином е непрекъснато диференцируема функция. Такива функции се наричат интерполиращи кубични сплайни.

Интерполиращ кубичен сплайн е функция S(x), за която