Задачи за динамични натоварвания
Технически портал, посветен на Sopromat и историята на неговото създаване
Архив на категория: Проблеми с динамично натоварване
Изчисляване на ударното натоварване
ТоварQ =1200N пада върху I-образна греда (№ 20) с дължина l=9m, свободно лежаща върху две твърди опори , от височинаh=5 cm.
Изисква се: намеретенай-високото нормално напрежение в гредата e и определетедеформацията на гредата в точката, където пада товарът.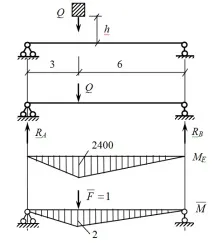
1) Изчисляваме гредата за действието настатично натоварване. Прилагаме силаQ и изграждамеграфиката на огъващите моменти МF. За да направим това, дефинирамереакциите :
Максималният момент ще бъде равен на:
2) Прилагамеединична сила към мястото, където пада товарът, и изграждаме единична диаграма (графика на моментите от единичен товар).
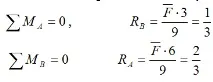
Максималният момент ще бъде равен на:
3) Определямемаксималното огъване на гредата в мястото, където товарът попада под статичното действие на товара, съгласно всеки изследванметод за определяне на преместванията. Например, споредправилото на Верещагин :
4) Определетединамичен коефициент :
5)Най-високо нормално напрежение в гредата при удар
6) Максимална деформация при удар:
Изчисление за удар при огъване
Конзолна греда, изработена от I-греда № 22 беше подложена наудар, когато товарътF=10kN падна в сечение C. Височина на паданеH=2 cm.
Намерете деформацията на свободния край на гредата.
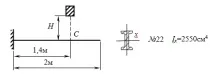
Тук ще трябва даопределите деформациите два пъти поради статичното действие на тежестта на падащия товар:деформацията в точка С, за да определите динамичния коефициент идеформацията на края на конзолата, за да отговорите на въпроса, зададен в задачата :
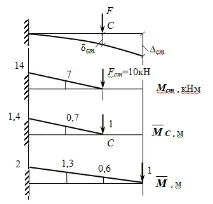
Чрез "умножаване" на диаграмите намираме :
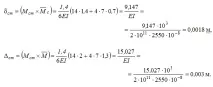
Динамично съотношение при удар
Тогавадинамичното отклонение на края на конзолата ще бъде:
Изчисляване на надлъжно въздействие
Оставете товараF=10kN да падне от височинаH=10cm върху I-образна стойкаℓ=4m.
Дефинирайте:
1) максимално нормално напрежение
2) най-голямото скъсяване на стойката при удар.
Да приемем, че багажникът не губи стабилност.
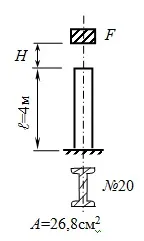
Решение.
Формулите за изчисляване на въздействието са:
къдетодинамичен коефициент при удар
- тези параметри съответстват на статичния метод за прилагане на силата на тежестта на падащия товар, т.е.
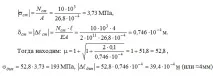
Трептения на системи с една степен на свобода
На двутавровата греда е монтиран електродвигател с теглоG=5kN, по време на работа на който поради дисбаланс на въртящите се части възниква вертикална центробежна сила със скорост на въртенеn=300 об/мин.
Определете най-големите нормални напрежения и деформация.
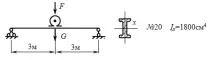
Решение:
Гредата е под действието на две натоварвания:статично натоварване - тегло на двигателя G идинамично (вибрационно) натоварване F. Следователно всички параметри са съставени отстатични и динамични компоненти :
Ще намерим статичните компоненти на силатаG както обикновено в статичното изчисление:
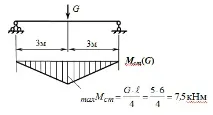
Най-голямотостатично напрежение в средната част на гредата ще бъде:
За да определим статичното отклонение на средната секция, избираме спомагателно състояние и изграждаме диаграма:
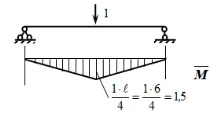
Деформацията поради статично натоварване G ще бъде:
Динамични стойности на параметрите от действиевибрационното натоварване се определя с помощта надинамичния фактор, както следва:
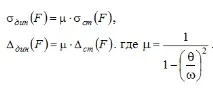
Формулата за динамичния коефициент на вибрационно натоварване включва стойносттаω -кръгова честота на собствените (свободни) трептения, определена по формулата:
където:g=9.81m/sec 2 –гравитационно ускорение,
Δst –отместване на точката на местоположението на осцилиращата маса (в този случай двигателя) от собственото й тегло.
Тогава стойносттана коефициента на динамично вибрационно натоварване ще бъде:
Туккръговата честота на самото вибрационно натоварване
След това намираме , за коетонай-голямата стойност на вибрационното натоварване се прилага към гредата по статичен начин:
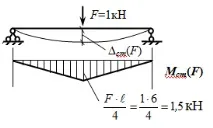
Деформацията на средата на участъка в греда върху две опори също може да се изчислиспоред добре известната формула:
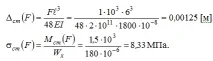
Тогавадинамичните стойности на необходимите параметри ще бъдат:
представляваамплитудата на колебанията на масата (двигателя), т.е. най-голямото отклонение от позицията на статично равновесие. Следователнонай-голямата стойност на отклонение е сумата от статичното изместване и амплитудата на трептене
Най-висок нормален стрес