Задайте изваждане, липса на комутативност и асоциативност
Разликата на множествата A - B е множеството от всички онези и само онези елементи от A, които не се съдържат в B. Или, което е същото, A - B = .
B не може да бъде подмножество на A.
Необходимо е да се обърне внимание на факта, че операцията за изваждане е некомутативна и неасоциативна, подобно на операцията за изваждане на числа в аритметиката. Липсата на комутативност е очевидна: i.
Нека докажем липсата на асоциативност. Нека покажем, че (A-B)-C не е равно на A-(B-C). Множеството от лявата страна се състои от елементи на множество A, които не са елементи нито на множество B, нито на множество C, т.е. съвпада с множеството A-(B U C) Множеството от дясната страна се състои от елементи на множеството A, които не са елементи на множеството B, но елементите, които са пресечната точка на множествата A, B и C, са включени в това множество, т.е. това множество е същото като множеството A-BU(A&B&C) .
5. Симетрична разлика, определения и свойства.
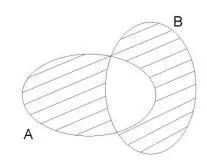
Симетричната разлика на две множества A и B е сумата от разликите A -B и
Б-А.
Това се означава като C = A /_\ B.
Забележете, че A/_\ B = (A UB) \ (B U A), защото симетричната разлика се състои от тези елементи на множествата A и B, които не принадлежат на A и B едновременно. Резултатът е набор от елементи на тези множества, които принадлежат само на едно от тях. Ще видим, че A /_\ B=(AUB)-(A&B), тъй като симетричната разлика се състои от тези елементи A и B, които не принадлежат на A и B едновременно.
Доказателство: ⇒ AΔB⊂(A∪B)\(A∩B), ∀x, x∈(A\B)∪(B\A) → x∈A\B или x∈B\A → (x∈A и x∉B) или (x∈B и x∉A) → 1) x∈A и x∉A∩B, 2) x∈ B и x∉A∩B → x∈(A∪B)\(A∩B); в обратна посока се доказвапо същия начин.
Имайте предвид, че тази операция е едновременно комутативна и асоциативна.
Не знам какво повече да напиша тук!
6.Operatsiya комплекти допълват, принципът на двойствеността.
Допълнението на множеството A, означено с A', е множеството от елементи на вселената, които не принадлежат на A. Следователно,
Ако основното множество се означи с S, то допълнението на множеството A е разликата S \ A (фиг. 8). Това се обозначава като CA или A с горна линия.
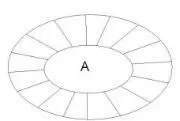
Фиг. 8 Допълнение към набор А
Пример. Ако разглеждаме множеството от всички цели числа като основно множество S, а множеството от четни числа като A, тогава допълнението на множеството A ще бъде множеството от нечетни числа.
Нека формулираме принципа на дуалността.
1) допълнението на обединението на две множества е равно на пресечната точка на добавките на тези множества:
Не (A UΒ) = (не A) & (не Б)
2) допълнението на пресечната точка на две множества е равно на обединението на допълненията на тези множества:
Не (A & B) = (не A) U (не B)
Нека докажем равенството (1).
Нека (x принадлежи на (не (A UB)), т.е. (x не принадлежи на (AUB)), така че x не принадлежи нито на множество A, нито на множество B, следователно (x принадлежи (не A)) и (x принадлежи (не B)), което означава, че (x принадлежи (не A) & (не B)). И така доказахме.