Закон Богуславски-Лангмюр
Законът на Богуславски-Лангмюр или законът за силата на трите секунди установява връзката между анодния ток и анодното напрежение във вакуумен диод. Тази зависимост за електроди с най-прости конструкции е изследвана през 1911 г. от американския учен К. Чайлд (K. Child), през 1913 г. от американския физик И. Лангмюр (I. Langmuir) и впоследствие прехвърлена към по-сложни случаи от С. А. Богуславски (1923 г., България), И. Лангмюр (1923 г.), К. Блоджет (K. Blodgett, 19 24). , САЩ). В чуждестранната литература законът носи името на Чайлд-Лангмюр.
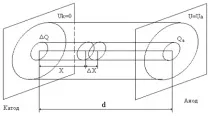
Фиг.8.2. Към заключението на закона за "степените на трите секунди"
Нека определим зависимостта на анодния ток от анодното напрежение в диод, образуван от две плоски, неограничени, успоредни пластини (фиг. 8.2). В този случай ефектът на ръба може да бъде пренебрегнат и полето между анода и катода може да се счита за равномерно. Ние приемаме следните предположения. Нека на повърхността на катода (x=0)Uk=0, , началната скорост на електронитеV0=0. Скоростта на електрона във всяка точка от междуелектродното пространство с потенциалU, акоV0=0, се определя от израза:
. (8.1)
Като се има предвид, че има пространствен заряд в междуелектродното пространство, използваме уравнението на Поасон, което за вакуум и при условие, чеEY=EZ =0, може да бъде записано като:
. (8.2)
Тукρ е обемната плътност на заряда (C/m 3 ), аε0=8,85∙10 -12 F/m е електрическата константа.
Както е известно, обемната плътност на заряда е свързана с плътността на тока чрез отношението:
, (8.3)
или, като се вземе предвид (8.1):
. (8,4)
Замествайки израза за ρ в (8.2), записваме уравнението на Поасон във формата:
. (8,5)
Умножаване на двете страни на равенствата по и интегриране от 0 доx,получаваме:
. (8,6)
Интеграционните константи са равни на нула, тъй като приx=0 UK=0иdU/dx=0.
Интегрирането (8.6) след вземане на корен от двете страни на равенството и разделяне на променливите води до следния резултат:
. (8,7)
От тук е лесно да се определи плътността на тока, която е еднаква за всяка част от междуелектродното пространство:
. (8,8)
Замествайкиx=dиU=Ua, записваме за плътността на тока на повърхността на анода:
. (8,9)
За да намерим стойността на анодния ток, умножаваме (8.9) по стойносттаQaна тази част от анодната повърхност, където попадат електроните:
, (8.10)
. (8.11)
Израз (8.11), който аналитично показва функциятаIa=f(Ua), се наричазакон на "степента на три секунди".