Знаков тест (биномен тест)
Знаковият тест е друг непараметричен метод, който ви позволява лесно да проверите дали независимата променлива е повлияла на производителността.
Трябва да се отбележи обаче, че ако броят на степените на свобода е по-голям от 1, тогава критерият / 2 не може да бъде приложен, когато в 20 процента или повече от случаите теоретичните честоти са по-малки от 5 или когато поне в един случай теоретичната честота е 0 (Siegel, 1956).
Статистика и обработка на данни 305
отказ от задачата от субектите. При този метод първо пребройте броя на субектите, чиито резултати са намалели, и след това го сравнете с броя, който може да се очаква въз основа на чиста случайност (в нашия случай вероятността за случайно събитие е 1: 2). След това определете разликата между тези две числа, за да разберете колко надеждна е тя.
При изчисляване резултатите, показващи увеличение на ефективността, се вземат със знак плюс, а намалението - със знак минус; случаите без разлика се игнорират.
Изчислението се извършва по следната формула:
Z=
където X е сумата от "плюсовете" или сумата от "минусите";
и / 2 - броят на смените в една или друга посока с чист шанс (един шанс от два 1);
0,5 корекционен фактор, който се добавя към X, ако X и/2.
Ако сравним в нашия опит ефективността на субектите преди експозиция (фон) и след експозиция, получаваме
Парти с опит
Фон: 12 21 10 15 15 19 17 14 13 11 20 15 15 14 17 След излагане: 8 20 6 8 17 10 10 9 7 8 14 13 16 11 12 Знак: ____-(-- ----_--)---
Така в 13 случая резултатите се влошиха, а в 2 се подобриха. Сега ни остава да изчислим Z за една от тези две X стойности:
(2+ 0,5) -
12,5 - 7,5 ^ZT^- 1'83'
' Такава вероятност е типична напр.за n хвърляния на монети. В случай, че n зара са разпръснати, тогава вероятността да изпаднете от едно или друго лице вече е равна на един шанс от 6 (nid).
406 Comfort B
От таблицата на Z стойностите можете да видите, че Z за ниво на значимост от 0,05 е 1,64. Тъй като получената от нас стойност на Z се оказа по-висока от табличната, нулевата хипотеза трябва да бъде отхвърлена; това означава, че под влиянието на независимата променлива окуломоторната координация наистина се е влошила.
Критерият за признаци е особено често използван при анализа на данните, получени в изследванията по парапсихология. С помощта на този критерий може лесно да се сравни например броят на така наречените телепатични или психокинетични реакции (X) (вижте досие 5.1) с броя на подобни реакции, които биха могли да се дължат на чиста случайност (u/2).
Други непараметрични критерии
Има и други непараметрични критерии, които ви позволяват да тествате хипотези с минимален брой изчисления.
Критерият за ранг ви позволява да проверите дали редът на събития или резултати е случаен или дали е свързан с действието на някакъв фактор, който не е взет предвид от изследователя. С помощта на този критерий е възможно например да се определи дали редът на редуване на мъже и жени в опашката е случаен.В нашия експеримент този критерий ще ни позволи да разберем дали лошите и добрите резултати на всеки субект от експерименталната група се редуват след излагане по някакъв определен начин или дали добрите резултати не падат главно в началото или в края на опитите.
При работа с този критерий първо се разграничават такива последователности, в които стойностите, по-малки от медианата, следват в ред, и тези, в които стойностите, по-големи от медианата, следват в ред. По-нататък в таблицата за разпределение R (от английските писти-последователности) проверете дали тези различни последователности се дължат само на случайност.
При работа с порядъчни данни 1 се използват непараметрични тестове като U теста на Mann-Whitney и T теста на Wilcoxon. U тестът ви позволява да проверите дали има значителна разлика между две независими проби, след като групираните данни от тези проби са класифицирани и класирани и сумата от ранговете за всяка извадка е изчислена. Що се отнася до критерия T, той се използва за зависими извадки и се основава както на класирането, така и на знака на разликите между всяка двойка данни.
Ще отнеме твърде много място, за да покажем прилагането на тези критерии с примери. При желание читателят може да се запознае с тях по-подробно, като използва специални ръководства.
1 Такива данни най-често се получават при класиране на количествени данни, които не могат да бъдат обработени с помощта на параметрични тестове.
Статистика и обработка на данни 307
Корелационен анализ
Когато изучават корелациите, те се опитват да установят дали има връзка между два показателя в една и съща извадка (например между височината и теглото на децата или между нивото на IQ и училищните постижения) или между две различни проби (например при сравняване на двойки близнаци) и ако тази връзка съществува, тогава дали увеличението на един показател е придружено от увеличение (положителна корелация) или намаление (отрицателна корелация) на другия.
С други думи, корелационният анализ помага да се установи дали е възможно да се предвидят възможните стойности на един индикатор, като се знае стойността на друг.
Досега, когато анализирахме резултатите от нашия опит в изучаването на ефектите на марихуаната, съзнателно пренебрегвахме такъв показател като времето за реакция. Междувременно щеше да бъдеинтересно е да се провери дали има "връзка между ефективността на реакциите и тяхната скорост. Това би позволило например да се твърди, че колкото по-бавен е човек, толкова по-точни и ефективни ще бъдат действията му и обратно.
За тази цел могат да се използват два различни метода: параметричният метод за изчисляване на коефициента на Bravais-Pearson (r) и изчисляването на коефициента на рангова корелация на Spearman (r), който се прилага към ординални данни, т.е. е непараметричен. Нека обаче първо разберем какво е коефициент на корелация.
Коефициент на корелация
Коефициентът на корелация е стойност, която може да варира от +1 до -1.В случай на пълна положителна корелация този коефициент е плюс 1, а в случай на пълна отрицателна - минус 1. На графиката това съответства на права линия, минаваща през точките на пресичане на стойностите на всяка двойка данни:
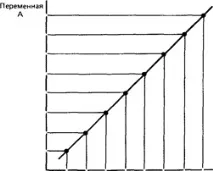
Обща положителна корелация (r = +1)
308 Приложение Б
| Променлива А | \ |
| ) ДА СЕ | |
| ^ | |
| \ | |
| \ | |
| ^ | |
| \ | |
| \ |
Пълна отрицателна корелация (/" ^-l)
Ако тези точки не се подредят в права линия, а образуват „облак“, абсолютната стойност на корелационния коефициент става по-малка от единица и се доближава до нула, когато облакът се закръгля:
Ако коефициентът на корелация е 0, двете променливи са напълно независими една от друга.
В хуманитарните науки една корелация се счита за силна, ако нейният коефициент е по-голям от 0,60; ако надвишава 0,90, тогава корелацията се счита за много силна. Въпреки това, за да можем да направим изводи за връзките между променливите, обемът е от голямо значение.проби: колкото по-голяма е извадката, толкова по-достоверна е стойността на получения коефициент на корелация. Има таблици с критични стойности на корелационните коефициенти на Bravais-Pearson и Spearman за различен брой степени на свобода (той е равен на броя на двойките минус 2, т.е. n - 2). Само ако коефициентите на корелация са по-големи от тези критични стойности, те могат да се считат за надеждни. И така, за да бъде надежден коефициентът на корелация от 0,70, най-малко 8 двойки данни (r = n - 2 = 6) трябва да бъдат взети в анализа при изчисляване на r (Таблица B.4) и 7 двойки данни (r = u - 2 = 5) при изчисляване на r (Таблица 5 в Приложение 6.5). - ——-
Статистика и обработка на данни
Съотношение Bravet-Pearson
_ (SXYj - nXY (n - 1)^5y
където XX Y е сумата от произведенията на данните от всяка двойка;
X-средно за променливата на данните X;
Y-средно за променлива данни Y;
дд - стандартно отклонение за разпределение x;
sy е стандартното отклонение за y разпределението. Сега можем да използваме този коефициент, за да определим дали има връзка между времето за реакция на субектите и ефективността на техните действия. Вземете например фоновото ниво на контролната група.