§1. Основни понятия на алгебрата.
1.1. Първоначални концепции.
Как започва една приказка? В Далечното кралство в Далечното кралство са живели и са били... Не само в приказките, но и в математиката и програмирането е важна средата, в която се развиват всички действия – обгръщащата вселена, средата за програмиране.
Нашите два основни обекта са числа и полиноми. Къде живеят? Както обикновено в математиката, те "живеят" в някакво множество, наречено алгебрична система.
Алгебрична системае непразно множество, съдържащо една или повече алгебрични операции.
Какво е алгебрична операция? Има много от тях, имаме нужда от двоична алгебрична операция.
Двоична алгебрична операциявърху множество A е всяко картографиране, което свързва всяка двойка елементи от множеството A с елемент от множеството A.
В този смисъл суми или произведения на числа, полиноми или матрици са алгебрични операции. Двоичните алгебрични операции обикновено се наричат събиране или умножение. Това е съкращение за дългата тирада "двоична алгебрична операция". Те също са етикетирани по различен начин. Ето най-често използваните обозначения: +, ·, ×, •, , , *.
Ако набор A съдържа 10 елемента, тогава ще има 100 двойки елементи. Тъй като всяка двойка от 100 може да бъде свързана с всеки от 10 елемента, тогава общият брой различни алгебрични операции върху набор от 10 елемента ще бъде 10 100. Както знаете, във видимата част на Вселената има около 10 50 атома, така че няма начин да се изучават всички алгебрични операции.
Дефиниция.Алгебричната операция "+" се нарича:
с неутрален елементакоe+a=a+e=a;
с обратими елементи, ако
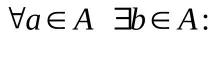
Много малко от алгебричните операции притежават поне едно от горните свойства, още по-малко и четирите.
Нека въведем нова алгебрична операция
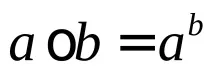
Пример 2.Върху множеството от естествени числа с добавена нула въвеждаме нова операция
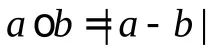
Дефиниция.Ако върху множество A е дадена асоциативна алгебрична операция, тогава такова множество се наричаполугрупа.Ако тази операция е комутативна, тогава полугрупата се наричакомутативна.
Пример 3.Наборът от естествени числа по отношение на обичайната операция събиране е комутативна полугрупа.
Дефиниция.Ако върху множество A е дадена асоциативна алгебрична операция с неутрален елемент, тогава такова множество се наричаполугрупа с идентичностилимоноид. Ако тази операция е комутативна, тогава моноидът се наричакомутативен.
Пример 4.Наборът от естествени числа по отношение на операцията обикновено умножение е комутативен моноид. Ако към естествените числа се добави нула, тогава чрез събиране получаваме комутативен моноид.
Тъй като чрез формално добавяне на неутрален елемент всяка полугрупа може да се превърне в моноид, тези понятия често не се разграничават.
Определение.Ако върху множеството A е дефинирана асоциативна операция, която има неутрален елемент и всички негови елементи имат обратни, тогава множеството A се наричагрупа. Ако операцията също е комутативна, тогава групата се наричакомутативнаилиабелевав чест на Нилс Хайнрих Абел (1802-1829).
Пример 5. Множеството от цели числа по отношение на операцията обикновено събиране е комутативна група. Множеството от ненулеви цели числа по отношение на операцията обикновено умножение е комутативен моноид, но не и група.
Пример 6. Множеството от ненулеви рационални числа по отношение на операцията обикновено умножение е комутативна група.
Как се нарича алгебрична операция - събиране или умножение, в случай, че е единствената, е напълно маловажно. Но ако има две операции, тогава добавянето обикновено се нарича тази, която е комутативна.
Сега се обръщаме към алгебрични системи, върху които са дадени две алгебрични операции. Ако тези операции не взаимодействат една с друга, тогава няма да възникне нищо съществено ново. Дали има извънземни на Земята или не, няма никакво значение, тъй като те не се месят в живота ни.
Определение.Нека върху множеството A са дадени две алгебрични операции. Една от операциите е асоциативна, комутативна, има неутрален елемент, а всички елементи на множеството A имат обратни. Нека го наречем добавяне. Втората операция, наречена умножение, е асоциативна. Операциите са свързани помежду си със закона за дистрибутивност
(a+b)c=ac+bc,c(a+b)=ca+cb,
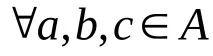
В този случай множеството A се нарича пръстен. Ако умножението е комутативно, тогава пръстенът се нарича комутативен.
Между другото, комутативните пръстени никога не се наричат абелеви.
По-точно, дистрибутивността, която въведохме, се нарича дистрибутивност на събирането по отношение на умножението. Операциите върху този имот са неравностойни. Ако разпределимостта на умножението по отношение на събирането също беше валидна, тогава формулите биха били верни
Комбинирайки двете дистрибутивности заедно, получаваме
Ако пръстенът съдържа неутрален елемент за умножение, той обикновено се нарича единица и се обозначава с 1 (да не се бърка с числото 1), след което, замествайки
с=1, получаваме това. Очевидно противоречие. Така справедливостта, т.е. симетрията на дефиницията на пръстен по отношение на събиране и умножение е принципно невъзможна.
Пример 7.Наборът от цели числа по отношение на обичайните операции събиране и умножение е комутативен пръстен.
Пример 8.Нека K е пръстен, наборът от полиноми K[x] в променливатаxс коефициенти от пръстена K е пръстен по отношение на обичайните операции на събиране и умножение на полиноми. Ако пръстенът K е комутативен, тогава пръстенът K[x] също е комутативен.
1. Ако съществува неутрален елемент, той е уникален.
2. Ако операцията е асоциативна и елементътaима обратен елемент, тогава той е и единственият и се обозначава с “-a”, ако операцията се нарича събиране, и “a-1” или “1/a”, ако операцията се нарича умножение.
3. В пръстена за неутрален елемент чрез събиране, наречен нула, равенството е изпълнено.
4. В пръстена за обратни елементи чрез събиране равенството е изпълнено.
1. Да предположим, че има два неутрални елементаxиy, тогава по дефиницията на неутралния елементxимамеxy=yи, от друга страна,xy=x. Така чеx=y.
2. Нека "b" и "c"– елементи, обратни на елемента "а". По силата на аксиомата за асоциативност имамеb=b1=b(ac)=(ba)c=1c=c.
3. Имаме 0а=(0+0)а=0а+0а, следователно 0а=0. Обърнете внимание, че това доказателство използва аксиомата за неутрален елемент по отношение на добавянето, аксиомата за наличие на обратен елемент по отношение на добавянето, разпределимостта и имплицитната асоциативност по отношение на добавянето. Има само четири аксиоми.
(Между другото, при редуцирането на двете части от елемента 0a, което извършихме в едно действие, всъщност бяха използвани три аксиоми - наличието на обратна на събирането, асоциативността на събирането, аксиомата на неутралния елемент. В детайли изглежда така>+0a, трябва
4. Първо доказваме, че (-а)b=-(ab). За да направите това, проверете дали елементът (-a)bе обратен на елементаab. Наистина,ab+(-a)b=(a-a)b=0a=0. Тук използвахме дистрибутивността, свойството обратно на събирането и свойството нула, както и точка 3 от нашето доказателство.
Сега, използвайки току-що получения резултат, изчисляваме
Когнитивното значение на следствието е, че то обяснява защо умножението по 0 винаги води до 0 и защо „минус с минус дава плюс“. И двете от тези свойства са валидни, ако четирите аксиоми са верни: асоциативност на добавяне, дистрибутивност, наличие на неутрален елемент и обратното на събирането.
От гледна точка на програмирането следствието, доказано по-горе, също е много полезно. Аксиомите са инструкции за асемблер, елементарни операции, реализирани хардуерно в процесора. Нашите обичайни трансформации, например кастингкато термини, или умножени по 0, са езикови команди на високо ниво. Ние всъщност действахме като компилатор. Полезно е да направите това поне веднъж, така че когато се промени средата за програмиране, това означава какво трябва да се преработи.
Пример 9.Нека K е пръстен, Mn(K) е набор от квадратни матрици с размерn×nс коефициенти от пръстена K. По отношение на обичайните операции на събиране и умножение на матрици, Mn(K) е пръстен.
Обърнете внимание, че за разлика от полиномния пръстен K[x], пръстенът Mn(K) не наследява комутативността от коефициентния пръстен K.
Пример 10.Да разгледаме набора от остатъци (остатъци)
Zn=n—1> от деление на естествено числоn.Нека въведем операциите събиране и умножение върху него
,
къдетоa+bиabозначават обичайното събиране и умножение на цели числа.
По отношение на въведените операции множеството Znе комутативен пръстен с единица.
Най-малкият пръстен и най-обичаният от програмистите е пръстенът Z2 = остатъци по модул 2. В това, което следва, няма да използваме нотацията , , а използваме обичайните плюс и точка.
Предупреждение.Често се приема, че акоn>m, тогава пръстенът Znсъдържа пръстена Zm. Това е вредно погрешно схващане. Разбира се, външно пръстенът Z5= изглежда като подмножество на пръстена Z8=. Но в първия пръстен 3 3=4, 3+3=1, а във втория 3 3=1, 3+3=6. Елемент 3 в първия пръстен се различава от елемент 3 във втория, както Вася Петров от Вася Иванов. Това са омоними – еднакво звучащи думи с различно значение.
И завършваме нашето кратко алгебрично въведение с дефиницията на поле.
Дефиниция.Комутативен пръстен с единица, в която всички ненулеви елементи имат обратен вумножението се нарича поле.
Пример 11.НаборътQот рационални числа с обичайните операции събиране и умножение е поле.
МножествотоRот реални числа с обичайните операции събиране и умножение е поле.
Остатъчният пръстен Zp, къдетоpе произволно просто число, е поле. (Ще докажем това по-късно).
Проверете дали полиномният пръстен K[x] не е поле. (Съвет: Кой многочлен е обратен наx2 чрез умножение?).
Проверете дали матричният пръстен Mn(K) заn>1 не е поле.