13.5. Феромагнетици.
Феромагнетиците са вещества, които имат спонтанно намагнитване, което силно се променя под въздействието на външни въздействия - магнитно поле, деформация, температура.
Феромагнетиците, за разлика от слабо магнитните диа- и парамагнетици, са силно магнитни вещества: вътрешното магнитно поле в тях може да бъде стотици пъти по-голямо от външното поле.
Феромагнетизъм се наблюдава в кристали на преходни метали - желязо, кобалт, никел, в някои редкоземни метали и сплави.
Основните разлики в магнитните свойства на феромагнетиците.
1) Нелинейна зависимост на намагнитването от силата на магнитното поле Н
Както може да се види от (фиг. 13.4), при H>gt; Наблюдава се HS магнитно насищане.
2) При H S, зависимостта на магнитната индукция B от H е нелинейна, а при H>gt; H S - линеен (фиг. 13.5)
Ориз. 13.5 3) Зависимостта на относителната магнитна проницаемост от H има комплекс
характер (фиг. 13.6), а максималните стойности на µ са много големи (10 3 ÷ 10 6 ).
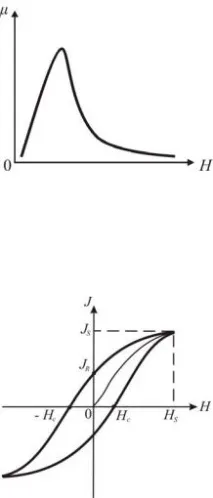
Ориз. 13.6 4) Всеки феромагнетик има такава температура, наречена Cur точка и,
над които това вещество губи своите специални магнитни свойства. 5) Наличие на магнитен хистерезис.
На (фиг. 13.7) е показана хистерезисна верига - графика на зависимостта на намагнитването на вещество от силата на магнитното поле H.
Намагнитването J S при H \u003d H S се нарича намагнитване на насищане. Намагнитването ± J R при H=0 се нарича остатъчно намагнитване (което
използвани за създаване на постоянни магнити)
Силата ± N от магнитното поле на напълно демагнетизиран феромагнетик се нарича коерцитивна сила. Той характеризира способността на феромагнетика да поддържа магнетизирано състояние.
Голямкоерцитивна сила (широка хистерезисна верига) се притежава от твърди магнитни материали, използвани за направата на постоянни магнити. Материалите, използвани за производството на трансформаторни сърцевини, имат ниска коерцитивна сила.
Измерването на жиромагнитното съотношение за феромагнетици показа, че елементарните носители на магнетизма в тях са спиновите магнитни моменти на електроните.
Тема 14. УРАВНЕНИЯ НА МАКСВЕЛ.
14.1. Пълен актуален закон.
14.2. ток на отклонение.
14.3. Единната теория на Максуел за електрическите и магнитните явления. Система от уравнения на Максуел.
14.4. Обяснения към теорията на класическата електродинамика. 14.5. Скоростта на разпространение на електромагнитното поле.
14.6. Релативистка интерпретация на магнитните явления (общи положения).
14.1. Пълен актуален закон.
Ако в който и да е проводник тече променлив ток - ток на проводимост, тогава вътре има променливо електрическо поле, т.е. ток на отклонение.
Магнитното поле на проводника се определя от общия ток:
В зависимост от електрическата проводимост на средата и честотата (полето) и двата термина играят различна роля:
в метали и при ниски честоти j cm проводник (в j cm не играе забележимо
в диелектриците и при високи честоти j cm играе основна роля.
И двата члена в уравнението на общия ток могат да имат еднакви знаци и противоположни. Следователно j full може да бъде по-голямо или по-малко от тока на проводимост или равно на нула.
Ако имаме отворен проводник, тогава само токът на проводимост се прекъсва в краищата му. Следователно, ако под ток разбираме пълния ток, тогава се оказва, че в природата всички променливи електрически токове са затворени. Това заключение е направено от Дж.
Максуел Джеймс Клерк (1831 - 1879) - най-великият английски физик. Работата му е посветенаелектродинамика, молекулярна физика, обща статика, оптика, механика, теория на еластичността. Установява статистически закон, описващ разпределението на газовите молекули по скорост. Най-голямото постижение на Максуел е теорията за електромагнитното поле, която той формулира като система от няколко уравнения, изразяващи всички основни закони на електромагнитните явления. Той също така формулира теорема в теорията на еластичността.
14.2. ток на отклонение.
Ако ключът е затворен (фиг. 14.1), тогава лампата няма да гори при постоянен ток: капацитетът C е прекъсване на веригата за постоянен ток. Но в моментите на включване лампата ще мига.
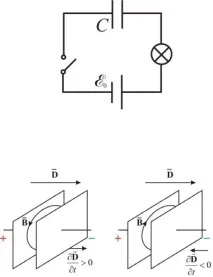
При променлив ток лампата гори, но в същото време ни е ясно, че електроните не преминават от една пластина в друга - между тях има изолатор (или вакуум). Но ако вземем устройство, което измерва магнитното поле, тогава в пролуката между плочите ще открием магнитно поле (фиг. 14.2).
Максуел нарича променливото електрическо поле ток на изместване. Защо е наречен така - ще видим по-нататък. Такъв термин има смисъл във веществата, например в диелектриците. Там зарядите се изместват от електрическо поле. Но във вакуум няма заряди - там няма какво да се движи, но има магнитно поле. Тоест, името на Максуел, "ток на преднапрежение" е неуспешно, но значението, вложено в него от Максуел
Максуел заключава, че всяко променливо електрическо поле генерира променливо магнитно поле.
Токовете на проводимост в проводник се затварят от токове на изместване в диелектрик или във вакуум. Променливо електрическо поле в кондензатор създава същото магнитно поле, както ако между плочите има ток на проводимост, със стойност, равна на тока в метален проводник.
Това твърдение позволява (въз основа на нашия пример скондензатор), за да намерите големината на тока на отклонение. По едно време ти и аз доказахме това повърхностно
плътността на поляризационните заряди σ е равна на D - векторът на електрическото изместване:
σ = Eεε 0, D = Eεε 0,
Общият заряд на повърхността на диелектрика и, следователно, на плочите
кондензатор q = σS (S е площта на облицовката)
т.е. токът на изместване е пропорционален на скоростта на промяна на вектора на електрическо изместване D.
Следователно той получи такова име - ток на пристрастие.
Плътност на тока на отклонение
Вихровото магнитно поле (B), генерирано от протичането на тока на изместване, е свързано с посоката на вектора ∂ ∂ D t по правилото на десния винт.
Какъв е токът на изместване?
Спомняме си, че ε = 1 + χ, където χ е диелектричната чувствителност на средата, ε е относителната диелектрична проницаемост. Ето защо:
D = r εε 0 E = (1 + χ) ε 0 E, т.е. D = ε 0 E + ε 0 Eχ.
Откъдето се вижда, че ε 0 χE = P l е поляризационният вектор. Следователно
В тази формула ε 0 ∂ ∂ E t
е плътността на тока на изместване във вакуум;
- поляризационна плътност на тока - плътност на тока, дължаща се на движението на зарядите в диелектрика. Този компонент на тока на отклонение генерира джаулова топлина (топлина, генерирана по време на UHF процедури,...). Токът на изместване във вакуум и в метали не излъчва джаулова топлина.
14.3. Единна теория на електрическите и магнитните явления. Система от уравнения на Максуел.
И така, променливото магнитно поле причинява появата на вихрово електрическо поле. Променливото електрическо поле предизвиква появата на магнитно поле. Тъй като се генерират взаимно, те могат да съществуват независимо от източниците на заряд или токове, които първоначално са създали един от тях. Накратко, това е електромагнитно поле (ЕМП). Превръщане на едно поле вдругото и разпространение в пространството - има начин на съществуване на ЕМП. Специфични прояви на ЕМП - радиовълни, светлина, γ - лъчи ...
И така през 1860г. Известният английски физик Джеймс Клерк Максуел създава единна теория за електрическите и магнитните явления, в която използва понятието ток на изместване, дефинира ЕМП и предрича съществуването на електромагнитно излъчване в свободното пространство, което се разпространява със скоростта на светлината.
Максуел формулира теорията за ЕМП като система от няколко уравнения. В теорията на електромагнетизма тези уравнения на Максуел играят същата роля като уравненията (или законите) на Нютон в механиката.

1). Като се има предвид явлението електромагнитна индукция, стигнахме до извода, че ЕМП на индукция ε i = ∫ E l ' d r l . Нека преминем от вихровото електрическо поле към магнитното: