2). Нека установим връзката между потенциала и интензитета на електростатичното поле във всяка точка от полето.

Разгледайте две точки 1 и2в еднородно електрическо поле (Фиг. 13) и приемете, че зарядът (+1) преминава от 1 към 2 по права линия Dl. Работата на електрическите сили DА по време на движение може да се изрази, първо, чрез напрегнатостта на полето: DА = ЕlDl.

От друга страна - чрез потенциалната разлика DU12.

`Е

El

2

Нека сегаувеличим потенциалапри движение `Dl, т.е. потенциална разлика DU21 на точка 2 (край на пътя) и точка 1 (начало на пътя), като ще го обозначим просто DU. Тогава

Приравнявайки двата израза за работа, получаваме израза за деня на напрегнатостта на електрическото поле:

В общия случай нанехомогеннополе и двете точки 1 и 2 трябва да бъдат избрани достатъчно близо една до друга, строго погледнато, безкрайно близо, така че E да може да се счита за константа на Dl. В границата при Dl®0,

Проекцията на вектора на напрегнатостта на електрическото поле върху дадена посока е равна наскоростта на промяна на потенциала в тази посока, взета с обратензнак.

Или използвайки идеята за градиента на скаларния град U:

`

=-град U,

тези. интензитетът във всяка точка на електростатичното поле е равен на потенциалния градиент в тази точка, взет с обратен знак.

В общия случай потенциалът U е функция и на трите декартови координати на разглежданата точка на полето, а

степен U = (

U/X)+ (U/Y)+ (U/Z).

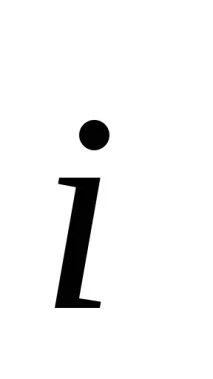
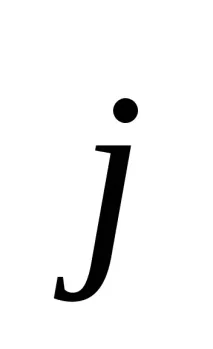
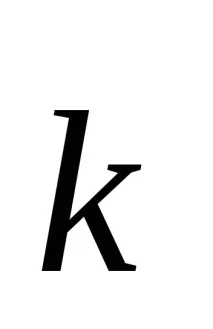
Следователно проекциите на вектора

върху координатните оси са свързани с потенциала на полето, така че:

Пример = -

U/X;EY = -U/Y;EZ = -U/Z;

Ако зарядът се движи в посока dl,перпендикулярна на силовата линия, т.е. перпендикулярно на `

, тогава cos (E,dl) = 0,E1l2 = 0 и dU/d1l2 = 0 или U=const.

Следователновъв всички точки на кривата, перпендикулярни на силовите линии, потенциалът е един и същ.

Геометричното място на точки с еднакъв потенциал се наричаеквипотенциална повърхност.

защото Ако потенциалът е постоянен само по кривите, ортогонални на линиите на полето, тогава еквипотенциалните повърхности трябва да бъдат навсякъде ортогонални на линиите на полето. Очевидно е, чеизвършената работапри преместване на електрически заряд по същата еквипотенциална повърхност е равна на нула.

Електрическото поле може да бъде представено графично не само с помощта на силови линии, но и с помощта на еквипотенциални повърхности. Безкраен брой еквипотенциални повърхности могат да бъдат начертани около всяка система от заряди. Обикновено те се извършват по такъв начин, че потенциалните разлики между всеки две съседни еквипотенциални повърхности да са еднакви.

Познавайки местоположението на силовите линии на електрическото поле, е възможно да се конструират еквипотенциални повърхности и, обратно, от известното местоположение на еквипотенциалните повърхности е възможно да се определи абсолютната стойност и посоката на вектора на напрегнатост на електростатичното поле във всяка точка на полето.

Начертайте плоски сечения на най-простите електрически полета: а) положителен точков заряд, б) дипол, в) два точкови заряда с еднакъв знак.

Плътността на еквипотенциалните линии е пропорционална на напрегнатостта на полето: където E е по-голямо, там еквипотенциалните линии са разположени по-близо една до друга.

---