§ 2. Вектор ред и вектор колона
Масивите са един от най-разпространените начини за съхраняване на данни и се използват във всички езици за програмиране и изчислителни пакети. Особеностите на работата с масиви в MatLab включват факта, че едномерният масив може да бъде вектор на ред или вектор на колона. Ако е важен начинът на представяне на масива, тогава ще наблегнем на това дали е ред или колона. Ако това не е от съществено значение, тогава ще говорим за вектори на редове и вектори на колони просто като вектори или едномерни масиви (едномерен масив в MatLab е двумерен, в който едно от измеренията е равно на единица).
За въвеждане на вектор се използват квадратни скоби, елементите на вектора са разделени един от друг:
точка и запетая, ако искате да получите колонен вектор;
интервал или запетая, ако искате да поставите елементите във векторния ред.
Вмъкване на вектори на колони и вектори на редове
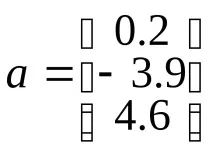
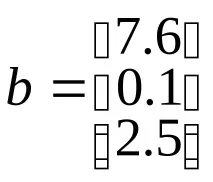
към съответните масиви, като напишете:
Точката и запетая в края на всеки ред е там, за да потисне показването, няма нищо общо с точката и запетая, която е разделителят на елементите във векторните колони. Отпечатайте стойностите на променливите a, b, u, v в командния прозорец и вижте как MatLab показва съдържанието на вектора на реда и вектора на колоната. Вземете информация за променливите с командата whos В предишния параграф забелязахте, че числата се съхраняват в двумерни масиви, всеки от които има размер 1. Векторите също се представят като двумерни масиви, един от размерите на които е равен на единица.
Функцията за дължина се използва за получаване на дължината на вектор, векторът е посочен като неин входен аргумент:
Векторите на колони с еднакъв брой елементи могат да се добавят и изваждат един от друг с помощта наЗнаци "+" и "-". Същото важи и за редовите вектори:
Добавянето и изваждането на вектор на ред и вектор на колона или вектори с различни размери води до грешка. Операцията * е предназначена за векторно умножение според правилото за умножение на матрици. Тъй като MatLab прави разлика между редови вектори и колонни вектори, е допустимо или да се умножи редов вектор по колонен вектор със същата дължина (скаларен продукт), или да се умножи колонен вектор по редов вектор (външен продукт, който води до правоъгълна матрица). Скаларното произведение на два вектора се връща от функцията точка, а векторното произведение се връща чрез кръстосано:
Разбира се, кръстосаното произведение е дефинирано само за вектори от три елемента.
Апострофът ' е запазен за операцията по транспониране. Ако векторът съдържа комплексни числа, тогава операцията ' води до комплексно спрегнат вектор. Когато изчислявате точковите и векторните произведения с функциите кръст и точка, не е необходимо да се гарантира, че и двата вектора са или колони, или редове. Резултатът е правилен, например, когато се извиква c=cross(a,b'), само c става вектор ред.
MatLab поддържа поелементни векторни операции. Наред с умножението по правилото за матрично умножение съществува операцията поелементно умножение .*(точка със звездичка). Тази операция се прилага към вектори с еднаква дължина и води до вектор със същата дължина като оригиналните, чиито елементи са равни на произведенията на съответните елементи на оригиналните вектори. Например, за векторите a и b, въведени по-горе, умножението по елементи води до следния резултат:
Разделянето елемент по елемент ./(наклонена точка) работи по подобен начин. Освен това операторът .\(обратна наклонена черта точка) извършва обратно разделяне по елементи, т.е.изразите a./b и b.\a са еквивалентни. Повдигането на елементите на вектора a на степени, равни на съответните елементи b, става с помощта на.^. За транспониране на вектори-редове или вектори-колони е предназначена комбинацията .' (точка с апостроф). Операции и. за реални вектори водят до същите резултати. Не е необходимо да се използват поелементни операции при умножаване на вектор по число и число по вектор, деление на вектор на число, събиране и изваждане на вектор и число. Когато изпълнявате например операция a*2, резултатът е вектор със същия размер като a, с удвоени елементи.
Векторите могат да бъдат аргументи на вградени математически функции като sin, cos и т.н. Резултатът е вектор с елементи, равни на стойността на извиканата функция от съответните елементи на оригиналния вектор, например:
Въпреки това, за да изчислим по-сложна функция на вектор от стойности, да речем
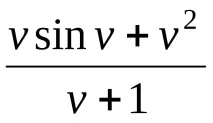
изразът f=(v*sin(v)+v^2)/(v+1) ще предизвика грешка дори когато се опитвате да умножите v по sin(v). Въпросът е, че v е вектор ред с дължина четири, тоест той се съхранява в двумерен масив с размер едно на четири. Sin(v) се представя по същия начин, следователно умножението със звездичка (според правилото за матрично умножение) е безсмислено. Подобна ситуация възниква при повдигане на квадрат на вектора v, т.е. всъщност при изчисляване на v*v. Правилният израз в MatLab изисква използването на елементни операции:
Често се изисква да се изчисли функция от вектор от стойности на аргументи, които се различават една от друга с постоянна стъпка. Предоставя се двоеточие за създаване на такива редови вектори. Последователност на командите
води до запълване на следните вектори:
-12,7922 3,1365 0,0997 0,1374 0,6744 1,2794 1,7832
стъпка може да бъдеотрицателна, в който случай първоначалната стойност трябва да бъде по-голяма или равна на крайната стойност, за да се получи непразен вектор. Ако стъпката е равна на единица, тогава тя може да бъде пропусната, например:
-3 -2 -1 0 1 2 3 4
Ясно е, че за да се запълни вектор-колона с елементи с постоянна стъпка, векторът-ред трябва да се транспонира. Създаването на вектори с двоеточие и възможността за извършване на операции по елементи са от съществено значение за визуализирането на масиви от данни, които ще бъдат обсъдени в следващите раздели.
MatLab има голям набор от вградени функции за обработка на векторни данни, някои от които са дадени в табл. 2.1. Пълен списък с налични функции се показва в командния прозорец с помощта на help datafun и за да получите подробна информация за всяка функция, трябва да посочите нейното име като аргумент на командата help. Имайте предвид, че редица функции могат да бъдат достъпни с един или два изходни аргумента. В случай на множество изходни аргументи, те се ограждат в квадратни скоби и се разделят един от друг със запетая.
Много често се изисква да се обработи само част от вектор или да се осъществи достъп до някои негови елементи. Нека анализираме правилата на MatLab, според които се индексират векторните данни. За достъп до елемент от вектор трябва да посочите номера му в скоби непосредствено след името на променливата, която съдържа вектора. Например сумата от първия и третия елемент на вектора v се намира с помощта на израза
Последният елемент на вектор може да бъде достъпен чрез end, т.е. v(end) и v(length(v)) водят до едни и същи резултати.