8 Алгоритми върху графики
Ec: y>:x,y eVl xФ y) -за неориентиран граф.
Ще използваме и обозначениятаV\ =n,E \ =m (кардиналност на множеството).
В теорията на графите класическият начин за представяне на графика е матрицата на инцидентите. Това е матрица A с n реда, съответстващи на върхове и m колони, съответстващи на ръбове. За насочен график колоната, съответстваща на дъгата (x, y) eE, съдържа +1 в реда, съответстващ на върха x, -1 в реда, съответстващ на върха y, и нули във всички останали редове. Loop, т.е. дъга от формата (x, x), е удобно да се представи друга стойност, например 2, в реда x.
За неориентиран график колоната, съответстваща на ръба, съдържа 1 в редовете, съответстващи на x и y, и 0 във всички останали редове (фиг. 28, фиг. 29).
n4= 6, m=7
0 0 0-1-10 о 0 0 0 0 11-1 0 0 0 0 0-11 (1.2) (1.3) (3.2) (3.4) (5.4) (5.6) (6.5) 28 Матрица на инциденти за насочен граф
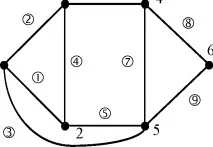
Ориз. 29 Матрица на инциденти за неориентиран граф
От алгоритмична гледна точка, матрицата на инцидентите е един от най-лошите начини за представяне на графика, защото:
необходими са n x m клетки от паметта, като повечето от клетките са заети с нули;
неудобен достъп до информация, т.к. отговори на въпросите: съществува ли дъгата (x,y)към кои върхове водят ръбовете от x? - изисква в най-лошия случай итерация на всички колони, т.е. m стъпки.
Малко по-добър начин за представяне на графика с матрица на съседствоB
размер n x m, където
bij= 1, ако има ребро, водещо от x към y, иbij= 0 в противен случай. Това предполага, че
ръб x,y> неориентираната графика върви както от x към y, така иот y до x. Следователно матрицата на съседство за неориентиран граф винаги е симетрична. За нашите графики матриците на съседство изглеждат така:
Основното предимство на матрицата на съседство е, че в една стъпка можете да отговорите на въпроса - има ли край от x до y?
Недостатъкът е фактът, че независимо от броя на ръбовете, обемът на заетата памет еn2 . На практика това неудобство понякога може да бъде коригирано чрез съхраняване на целия ред или колона в една машинна дума (за малкиn).
По-икономичен от гледна точка на паметта (особено за разредени графи, когатоmе много по-малко отn2 ) е начин за представяне на графика с помощта на списък от двойки, съответстващи на нейните ребра. Двойката (x,y) съответства на дъгата (x,y), ако графиката е насочена, и на ръба x,y>, ако графиката е неориентирана. В нашия случай списъците с двойки:
Очевидно в този случай обемът на паметта е 2t. Неудобството е голям брой стъпки (от порядъка на m в най-лошия случай) за намиране на множеството от върхове, към които водят ребрата от даден връх.
Ситуацията може да бъде значително подобрена чрез подреждане на набора от двойки лексикографски. След това можете да приложите двоично търсене.
Най-доброто решение в много случаи е структура от данни, която ще наричаме списъци с инциденти. Той съдържа за всеки връхVeVсписък от върховеи, така чеV—> иза насочен граф иV-иза неориентиран граф. Всеки елемент от такъв списък е записr, състоящ се от две полета:
d.line - горната част на графиката;
d.next - указател към следващия запис в списъка.
За последния запис в списъка - r.next = nil. Указател към началото на всекиСписъкът се съхранява в таблицата START. Така START[v] е указател към началото на списък, съдържащ върхове от набора за насочен граф, или > за неориентиран граф, съответно.
Целият списък ще бъде обозначен (неформално) LIST[y], а цикълът, който изпълнява някаква операция върху всеки елементиот този списък, ще бъде написан като
за ueLIST[v] do .
Обърнете внимание, че за неориентирана графика, всяко ребро v> представен два пъти:
през горнияvв списъка LIST[s] и
през горнитеив списъка LIST[y].
За нашите примери списъкът с инциденти LIST[y], veV изглежда така:
В много алгоритми структурата на графиката се променя динамично чрез добавяне и премахване на ръбове. В такива случаи приемаме, че в списъка LIST[u] елементът, съдържащ върха v, е снабден с указател към елемента от списъка LIST[v], съдържащ върха u, че всеки елемент от списъка е снабден с указател не само към следващия, но и към предишния елемент. След това, премахвайки някой елемент от списъка, можем лесно да премахнем друг елемент, представляващ същото ребро в ограничен брой стъпки, без да разглеждаме списъка, съдържащ този елемент.
Броят на клетките на паметта, необходими за представяне на графика с помощта на списъци с инциденти, е от порядък (n + m).
оператор P за всички елементи x X в произволна последователност
Нека обсъдим някои концепции, свързани с писането на алгоритми. Алгоритмите ще бъдат написани на неформален език, който използва основните конструкции на Pascal. Ако изпълнението на някой фрагмент от алгоритъма е очевидно, тогава такъв фрагмент ще бъде написан на естествен език. Ще използваме и някои неофициални конструкции, например:
има C константи,N, така че f(n) N
g(n) - някаква дадена функция има константи С, N, така че f(n) >С g(n) за всяко n>N Това се чете: 0(g(n)) - "от порядък най-много g(n)"
Q(g(n)) - "от порядък не по-малък от g(n)" Същото за функцията /n, m).
Калкулатор
Услуга за безплатна оценка на цената на работата
- Попълнете заявление. Експертите ще изчислят цената на вашата работа
- Изчисляването на цената ще дойде по пощата и SMS
Номерът на вашето приложение
Точно сега по пощата ще бъде изпратено автоматично писмо за потвърждение с информация за приложението.