8. АЛГОРИТМИ ЗА БЪРЗО ТРАНСФОРМИРАНЕ НА ФУРИЕ
8.1. ДЕФИНИЦИЯ И КЛАСИФИКАЦИЯ НА FFT АЛГОРИТМИ
Алгоритмите за бързо преобразуване на Фурие (FFT) са методи за бързо изчисляване на DFT, които елиминират изчислителната излишност, присъща на DFT. Те са предложени за първи път през 1965 г. от американците Cooley и Tukey и са сред основните DSP алгоритми в честотната област. Алгоритмите се основават на свойствата на комплекса
и периодичност W kn
период, равен на дължината на изпълнението на обработения сигнал N (броя FFT точки). Като се вземе предвид последното свойство, степента W N pkn = W N kn / p
съответства на периода N/p, където p са цели числа, които делят N. Използването на тези свойства в FFT алгоритми елиминира голям брой операции, които се повтарят при изчисляване на DFT.
Общият принцип на FFT е да се раздели DFT на оригиналната последователност на DFT от подпоследователности с по-малка дължина, до минималната възможна (равна на основата на FFT), чрез която се изчислява DFT на оригиналната последователност.
Разделянето означава децимиране на последователности във времевата или честотната област. В това отношение се прави разлика между унищожено във времето FFT и унищожено в честота FFT.
За разлика от DFT, FFT може да се изчисли само върху определен брой точки N, съответстващи на целочислената степен на неговата основа m: N = m L, където L е броят на стъпките на децимация: L = log m N. Най-използваните са FFT в бази m = 2, 4, 8, но най-често се използва FFT в база 2.
Както е показано в [40], глава 5, обратното DFT (IDFT) също се изчислява с помощта на FFT.
8.2. FFT АЛГОРИТЪМ С ОСНОВНО 2 ВРЕМЕВО МИСЛЕНЕ
Нека е дадена последователност x(n) N с крайна дължина N, n = 0, 1,.N – 1.
Трябва да намерим неговата DFT: X ( jk ) = ∑ x( n )W N kn за k = 0, 1. N– 1 (числа n = 0
контейнери на DFT) с минимално количество изчисления.
Решението на този проблем в този FFT алгоритъм е както следва.
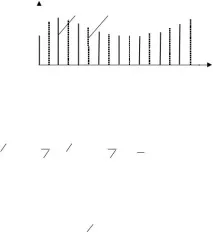
Разделяме началната последователност x(n) с дължина N на 2 подпоследователности с дължина N/2 – четни (включително проби x(n) с
четни индекси n: x 1 (n) = x (2n) и нечетни: x 2 (n) = x (2n + 1), n = 0,
1. (N/2) – 1. Това съответства на първото децимиране на сигнала
0 1 2 3 4 5 6 7 8 9 10 N – 1
Ориз. 8.1. Илюстрация за децимация на времето
Нека обозначим техните DFT като X 1 (jk) N/2 и X 2 (jk) N/2. Нека изразим DFT на оригиналната последователност x(n) N по отношение на DFT на подпоследователностите x 1 (n) N/2, x 2 (n) N/2:
N k = X 1 ( jk + ) W N K X 2 ( jk ), (8.1)
Това са първите N/2 честотни проби на DFT.
Втората половина на честотните проби X(jk) за k = (N/2), … (N – 1) може да бъде намерена, като се вземе предвид свойството на периодичност:
Изрази (8.1), (8.2) дефинират основната FFT операция (операция
фактор W N k , равен по абсолютна стойност на единица, се нарича
обръщане . Изчисленията по (8.3) включват едно комплексно умножение и двойка
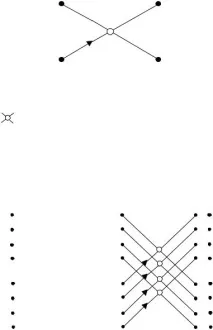
Основната операция е представена графично с помощта на сигнална графика (FFT бътерфлай), фиг. 8.2.
Ориз. 8.2. Графика на основния оперативен сигнал на FFT
допълнение (горен изход) и
съответства на умножение по
фактор на обръщане W N k .
Сигналната графика на FFT алгоритъма се получава като набор от графики на основни операции. За първия етап на изтъняване е показано на фиг. 8.3 за случая N = 8.
Ориз. 8.3. FFT графика на сигнала за първия етап на децимация
Нека оценим необходимото количество изчисления в съответствие с тази графика чрез броя на операциите за умножение:
за DFT K интелигентен DFT = N 2 ; за FFT K интелигентно FFT = 2( N /2) 2 + N /2 = N 2 /2 + N /2.
Както можете да видите, в резултат на едно изтъняване, количеството на изчисленията намаля с около 2 пъти.
Освен това, всяка от последователностите x 1 (n) и x 2 (n) може да бъде разделена на още две подпоследователности с половината от дължината: x 11 (n), x 12 (n) и x 21 (n), x 22 (n) (четни и нечетни) и повторете горните операции за комбиниране на техните DFT с помощта на основни операции. Такова изтъняване
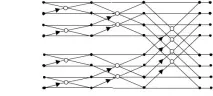
изпълняваме L пъти, докато получим N/2 последователности от две точки x l (0), x l (1), чието DFT е тривиално изчислено: X l (j0) = x l (0) + W 2 0 x l (1), X l (j1) = x l (0) − W 2 0 x l (1). В резултат на това получаваме пълната графика на FFT, показана на фиг. 8,4 за N = 8.
xp(1) = x(4) xp(2) = x(2)
x p (4) = x(1) x p (5) = x(5) x p (6) = x(3) x p (7) = x(7)
Ориз. 8.4. Пълна FFT графика за N = 8
В съответствие с графиката, на всеки от L етапа на DFT се изпълняват N/2 основни операции, а общият обем на изчисленията за сложни операции умножение и събиране - изваждане е:
log 2 N, K пъти FFT = NL = N log 2 N.
Броят на операциите с реални числа е 4 пъти по-голям за умножение и 2 пъти по-голям за усилване на FFT спрямо DFT по отношение на броя операции на умножение K мин. DFT / K мин. FFT = 2N / log 2 N. Така че, за
N = 2 10 = 1024 K umnFFT = 5120, K umnDFT ≈ 10 6, усилването е 204,8.
Подчертано на фиг. 8.4 възлови точки на графиката съответстват на клетките на оперативната сигнална памет. Тъй като изчисленията се извършват на етапи, е възможно да се заменят клетките на паметта, което определя общата необходима памет на сигнала в количество, равно на 2N клетки за N
комплексни числа (техните реални и имагинерни части). В този случай клетките на паметта, използвани на входа на графикатас N извадки от входния сигнал x(n) (обикновено комплексни) в крайна сметка се заменят с N комплексни честотни извадки на FFT X(jk) .
Характеристика на FFT алгоритъма с децимация на времето е неестественият ред на проби от входния сигнал, изискван от него,
поради множеството си разделения на четни и нечетни (n = 0, 4, 2, 6, 1, 5, 3, 7 за N = 8). Този ред на последователност се нарича Това води до необходимостта от предварително пренареждане на показанията на оригиналната последователност преди началото на изчисленията. За да направите това, естествените примерни числа на последователността x(n) се представят в двоичен код, тези кодове се четат в обратен ред, т.е. отдясно наляво и се преобразуват
след това обратно към десетична форма, съответстваща на броя на пермутираната последователност x(p).
Например, за графиката на фиг. 8.4 брой n (10) = 4 от оригиналната последователност x(n) в десетичната система съответства на двоичния код
n (2) = 100, (обърнат) код n dv.inv. = 001 и десетично число p = 1 от броя на пермутираната последователност x(p) .
8.3. АЛГОРИТЪМ ЗА РЕАЛИЗИРАНЕ НА СОФТУЕР FFT
ДЕЦИМИРАНА ВРЕМЕ БАЗА 2
Етапи на DFT в съответствие с графиката на сигнала на фиг. 8.4 следвайте в обратен ред стъпките на децимация на сигнала, извършени в изхода на FFT алгоритъма. На първия етап се изчисляват N /2 двуточкови DFT, всеки от които съответства на една основна операция на FFT, на втория, чрез комбинирането им по двойки с помощта на две
изчислени основни операции N /4
четириточкови DFT и др
използвайки N/2 основни операции
се комбинират в DFT на оригиналната последователност. Като се вземе предвид посочената закономерност, процесът на софтуерно изчисляване на FFT може да бъде разделен на три вложени цикъла(по ред на вмъкване):
по номера на изчислителния етап – DFT съюз i = 1, 2,…L (външен);
по броя на изчислените DFT на етап l = 1, 2, …2 L – i ;
по номера на основната операция на изчисленото DFT m = 1, 2, …2 i – 1 . Стойностите на факторите на обръщане за основната операция на етапа
се определят от обобщения израз
L − i , k = 0, 1, . ( N /(2 L – i + 1 ) ) –
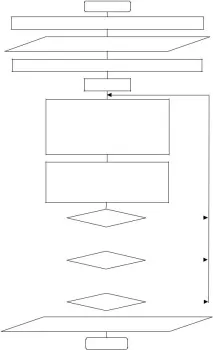
Описание на променливите: X(n), W, T, P1, P2, P3, i, l, m и т.н.
Вход за масив X(n), n = 0, 1, …N – 1
Пермутации: X(p) = X(n) n = p (dv.inv) , p = 0, 1, …N – 1
фактор на обръщане: P1 = ( m – 1) + (l – 1)2 i